Menu Close

3sinx-4cosx-4sinx-3cosx-dx-

Tinku Tara 0 Comments
Pin




Question Number 69502 by 20190927 last updated on 24/Sep/19
∫((3sinx+4cosx)/(4sinx+3cosx))dx
$$\int\frac{\mathrm{3sinx}+\mathrm{4cosx}}{\mathrm{4sinx}+\mathrm{3cosx}}\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 24/Sep/19
let I =∫ ((3sinx +4cosx)/(4sinx +3cosx))dx changement tan((x/2))=t give I =∫((3((2t)/(1+t^2 ))+4((1−t^2 )/(1+t^2 )))/(4((2t)/(1+t^2 )) +3((1−t^2 )/(1+t^2 ))))((2dt)/(1+t^2 )) =2∫((6t+4−4t^2 )/((8t+3−3t^2 )(1+t^2 )))dt =4 ∫ ((−2t^2 +3t +2)/((t^2 +1)(−3t^2 +8t +3)))dt =4 ∫ ((2t^2 −3t−2)/((t^2 +1)(3t^2 −8t−3)))dt let decompose F(t)=((2t^2 −3t−2)/((t^2 +1)(3t^2 −8t −3))) 3t^2 −8t −3 =0 →Δ^′ =16+9 =25 ⇒t_1 =((4+5)/3) =3 t_2 =((4−5)/3) =−(1/3) ⇒F(t) =((2t^2 −3t−2)/((t−3)(t+(1/3))(t^2 +1))) =(a/(t−3)) +(b/(t+(1/3))) +((ct +d)/(t^2 +1)) a =lim_(t→3) (t−3)F(t) =((18−9−2)/((3+(1/3))(10))) =((21)/(100)) b =lim_(t→−(1/3)) (t+(1/3))F(t) =((2(1/9)+1−2)/((−(1/3)−3)((1/9)+1))) =(((2/9)−1)/((−100)/(27))) =((−7)/9)×((−27)/(100)) =((7.9.3)/(9.100)) =((21)/(100)) lim_(t→+∞) t F(t) =0 =a+b +c ⇒c=−a−b =−((42)/(100)) =−((21)/(50)) we find d by calculating F(0) ⇒ ∫ F(t)dt =aln∣t−3∣ +bln∣t+(1/3)∣ +(c/2)ln(t^2 +1)+d arctan(t) +c =aln∣tan((x/2))−3∣+bln∣tan((x/2))+(1/3)∣ +(c/2)ln(1+tan^2 ((x/2))) +(dx/2) +c....
$${let}\:{I}\:=\int\:\:\frac{\mathrm{3}{sinx}\:+\mathrm{4}{cosx}}{\mathrm{4}{sinx}\:+\mathrm{3}{cosx}}{dx}\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int\frac{\mathrm{3}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{4}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{4}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{3}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\int\frac{\mathrm{6}{t}+\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} }{\left(\mathrm{8}{t}+\mathrm{3}−\mathrm{3}{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=\mathrm{4}\:\int\:\:\frac{−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{3}{t}\:+\mathrm{2}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(−\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{8}{t}\:+\mathrm{3}\right)}{dt}\:=\mathrm{4}\:\int\:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{2}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}−\mathrm{3}\right)}{dt} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)=\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{2}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}\:−\mathrm{3}\right)} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}\:−\mathrm{3}\:=\mathrm{0}\:\rightarrow\Delta^{'} =\mathrm{16}+\mathrm{9}\:=\mathrm{25}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{4}+\mathrm{5}}{\mathrm{3}}\:=\mathrm{3} \\ $$$${t}_{\mathrm{2}} =\frac{\mathrm{4}−\mathrm{5}}{\mathrm{3}}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow{F}\left({t}\right)\:=\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{2}}{\left({t}−\mathrm{3}\right)\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{{a}}{{t}−\mathrm{3}}\:+\frac{{b}}{{t}+\frac{\mathrm{1}}{\mathrm{3}}}\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow\mathrm{3}} \left({t}−\mathrm{3}\right){F}\left({t}\right)\:=\frac{\mathrm{18}−\mathrm{9}−\mathrm{2}}{\left(\mathrm{3}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{10}\right)}\:=\frac{\mathrm{21}}{\mathrm{100}} \\ $$$${b}\:={lim}_{{t}\rightarrow−\frac{\mathrm{1}}{\mathrm{3}}} \:\:\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right){F}\left({t}\right)\:=\frac{\mathrm{2}\frac{\mathrm{1}}{\mathrm{9}}+\mathrm{1}−\mathrm{2}}{\left(−\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{3}\right)\left(\frac{\mathrm{1}}{\mathrm{9}}+\mathrm{1}\right)}\:=\frac{\frac{\mathrm{2}}{\mathrm{9}}−\mathrm{1}}{\frac{−\mathrm{100}}{\mathrm{27}}} \\ $$$$=\frac{−\mathrm{7}}{\mathrm{9}}×\frac{−\mathrm{27}}{\mathrm{100}}\:=\frac{\mathrm{7}.\mathrm{9}.\mathrm{3}}{\mathrm{9}.\mathrm{100}}\:=\frac{\mathrm{21}}{\mathrm{100}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:+{c}\:\Rightarrow{c}=−{a}−{b}\:=−\frac{\mathrm{42}}{\mathrm{100}}\:=−\frac{\mathrm{21}}{\mathrm{50}} \\ $$$${we}\:{find}\:{d}\:{by}\:{calculating}\:{F}\left(\mathrm{0}\right)\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:={aln}\mid{t}−\mathrm{3}\mid\:+{bln}\mid{t}+\frac{\mathrm{1}}{\mathrm{3}}\mid\:+\frac{{c}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)+{d}\:{arctan}\left({t}\right)\:+{c} \\ $$$$={aln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{3}\mid+{bln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\mid\:+\frac{{c}}{\mathrm{2}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$+\frac{{dx}}{\mathrm{2}}\:+{c}…. \\ $$
Commented by 20190927 last updated on 25/Sep/19
thank you all for do this problem
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all}\:\mathrm{for}\:\mathrm{do}\:\mathrm{this}\:\mathrm{problem} \\ $$
Answered by $@ty@m123 last updated on 24/Sep/19
Answered by MJS last updated on 24/Sep/19
∫((3sin x +4cos x)/(4sin x +3cos x))dx= =(3/4)∫dx+(7/(16))∫(dx/((3/4)+tan x))= (1) (3/4)∫dx=(3/4)x (2) (7/(16))∫(dx/((3/4)+tan x))= [t=tan x → dx=(dt/(t^2 +1))] =(7/(16))∫(dt/((t+(3/4))(t^2 +1)))= =(7/(25))∫(dt/(t+(3/4)))−(7/(25))∫(t/(t^2 +1))dt+((21)/(100))∫(dt/(t^2 +1))= =(7/(25))ln (t+(3/4)) −(7/(50))ln (t^2 +1) +((21)/(100))arctan t = =(7/(25))ln ((t+(3/4))/( (√(t^2 +1)))) +((21)/(100))arctan t = =(7/(25))ln (sin x +(3/4)cos x) +((21)/(100))x =((24)/(25))x+(7/(25))ln (4sin x +3cos x) +C
$$\int\frac{\mathrm{3sin}\:{x}\:+\mathrm{4cos}\:{x}}{\mathrm{4sin}\:{x}\:+\mathrm{3cos}\:{x}}{dx}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\int{dx}+\frac{\mathrm{7}}{\mathrm{16}}\int\frac{{dx}}{\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{tan}\:{x}}= \\ $$$$ \\ $$$$\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{4}}\int{dx}=\frac{\mathrm{3}}{\mathrm{4}}{x} \\ $$$$ \\ $$$$\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\frac{\mathrm{7}}{\mathrm{16}}\int\frac{{dx}}{\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{tan}\:{x}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{16}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{3}}{\mathrm{4}}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{25}}\int\frac{{dt}}{{t}+\frac{\mathrm{3}}{\mathrm{4}}}−\frac{\mathrm{7}}{\mathrm{25}}\int\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}+\frac{\mathrm{21}}{\mathrm{100}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{25}}\mathrm{ln}\:\left({t}+\frac{\mathrm{3}}{\mathrm{4}}\right)\:−\frac{\mathrm{7}}{\mathrm{50}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{\mathrm{21}}{\mathrm{100}}\mathrm{arctan}\:{t}\:= \\ $$$$\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{25}}\mathrm{ln}\:\frac{{t}+\frac{\mathrm{3}}{\mathrm{4}}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\:+\frac{\mathrm{21}}{\mathrm{100}}\mathrm{arctan}\:{t}\:= \\ $$$$\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{25}}\mathrm{ln}\:\left(\mathrm{sin}\:{x}\:+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\:{x}\right)\:+\frac{\mathrm{21}}{\mathrm{100}}{x} \\ $$$$ \\ $$$$=\frac{\mathrm{24}}{\mathrm{25}}{x}+\frac{\mathrm{7}}{\mathrm{25}}\mathrm{ln}\:\left(\mathrm{4sin}\:{x}\:+\mathrm{3cos}\:{x}\right)\:+{C} \\ $$
Answered by $@ty@m123 last updated on 24/Sep/19
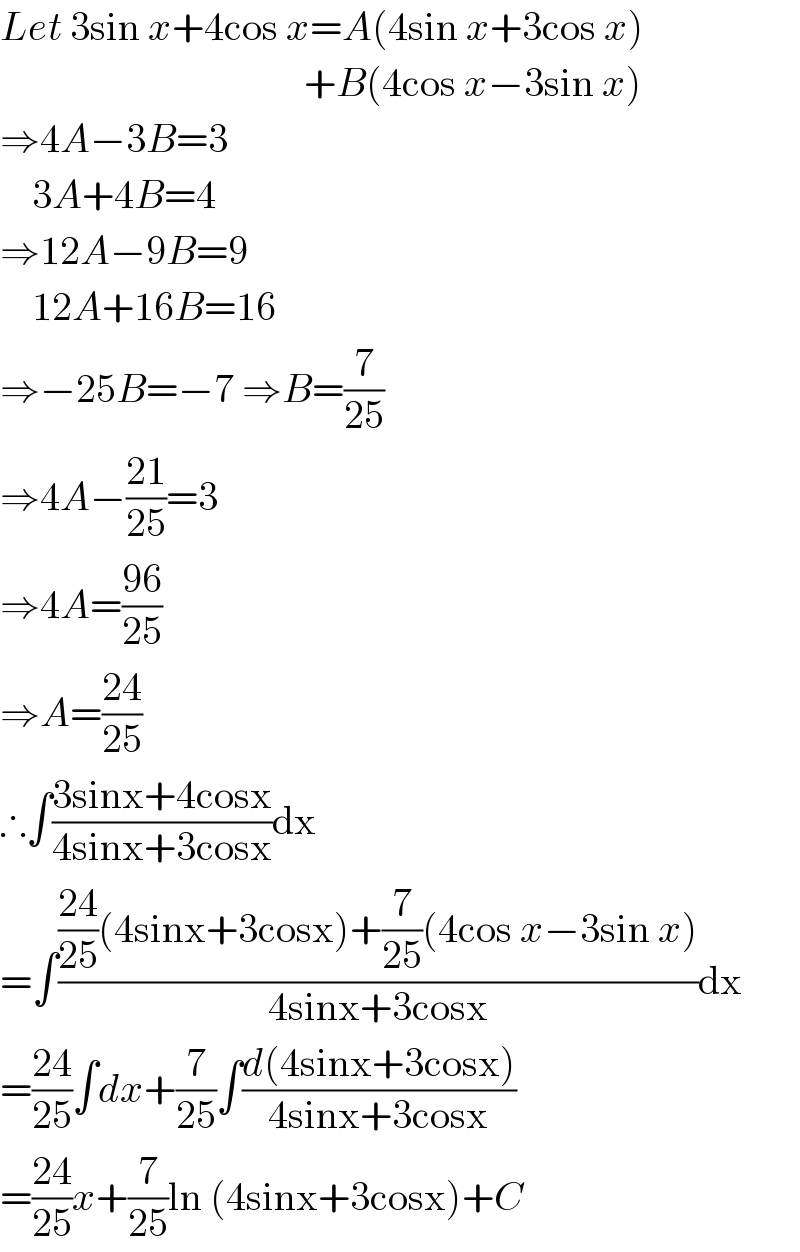
Let 3sin x+4cos x=A(4sin x+3cos x) +B(4cos x−3sin x) ⇒4A−3B=3 3A+4B=4 ⇒12A−9B=9 12A+16B=16 ⇒−25B=−7 ⇒B=(7/(25)) ⇒4A−((21)/(25))=3 ⇒4A=((96)/(25)) ⇒A=((24)/(25)) ∴∫((3sinx+4cosx)/(4sinx+3cosx))dx =∫((((24)/(25))(4sinx+3cosx)+(7/(25))(4cos x−3sin x))/(4sinx+3cosx))dx =((24)/(25))∫dx+(7/(25))∫((d(4sinx+3cosx))/(4sinx+3cosx)) =((24)/(25))x+(7/(25))ln (4sinx+3cosx)+C
$${Let}\:\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}={A}\left(\mathrm{4sin}\:{x}+\mathrm{3cos}\:{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{B}\left(\mathrm{4cos}\:{x}−\mathrm{3sin}\:{x}\right) \\ $$$$\Rightarrow\mathrm{4}{A}−\mathrm{3}{B}=\mathrm{3} \\ $$$$\:\:\:\:\mathrm{3}{A}+\mathrm{4}{B}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{12}{A}−\mathrm{9}{B}=\mathrm{9} \\ $$$$\:\:\:\:\mathrm{12}{A}+\mathrm{16}{B}=\mathrm{16} \\ $$$$\Rightarrow−\mathrm{25}{B}=−\mathrm{7}\:\Rightarrow{B}=\frac{\mathrm{7}}{\mathrm{25}} \\ $$$$\Rightarrow\mathrm{4}{A}−\frac{\mathrm{21}}{\mathrm{25}}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{4}{A}=\frac{\mathrm{96}}{\mathrm{25}} \\ $$$$\Rightarrow{A}=\frac{\mathrm{24}}{\mathrm{25}} \\ $$$$\therefore\int\frac{\mathrm{3sinx}+\mathrm{4cosx}}{\mathrm{4sinx}+\mathrm{3cosx}}\mathrm{dx} \\ $$$$=\int\frac{\frac{\mathrm{24}}{\mathrm{25}}\left(\mathrm{4sinx}+\mathrm{3cosx}\right)+\frac{\mathrm{7}}{\mathrm{25}}\left(\mathrm{4cos}\:{x}−\mathrm{3sin}\:{x}\right)}{\mathrm{4sinx}+\mathrm{3cosx}}\mathrm{dx} \\ $$$$=\frac{\mathrm{24}}{\mathrm{25}}\int{dx}+\frac{\mathrm{7}}{\mathrm{25}}\int\frac{{d}\left(\mathrm{4sinx}+\mathrm{3cosx}\right)}{\mathrm{4sinx}+\mathrm{3cosx}} \\ $$$$=\frac{\mathrm{24}}{\mathrm{25}}{x}+\frac{\mathrm{7}}{\mathrm{25}}\mathrm{ln}\:\left(\mathrm{4sinx}+\mathrm{3cosx}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *