Question Number 68970 by Peculiar last updated on 17/Sep/19

$$\int\frac{\mathrm{3}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{15}} }\:{dt} \\ $$
Answered by Kunal12588 last updated on 17/Sep/19
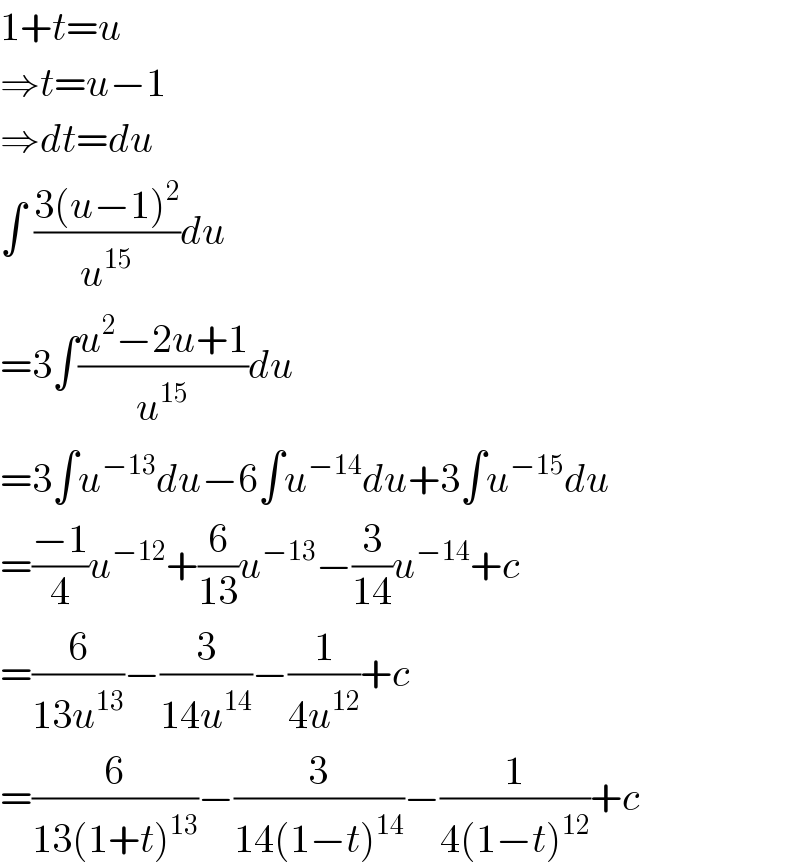
$$\mathrm{1}+{t}={u} \\ $$$$\Rightarrow{t}={u}−\mathrm{1} \\ $$$$\Rightarrow{dt}={du} \\ $$$$\int\:\frac{\mathrm{3}\left({u}−\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{15}} }{du} \\ $$$$=\mathrm{3}\int\frac{{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{1}}{{u}^{\mathrm{15}} }{du} \\ $$$$=\mathrm{3}\int{u}^{−\mathrm{13}} {du}−\mathrm{6}\int{u}^{−\mathrm{14}} {du}+\mathrm{3}\int{u}^{−\mathrm{15}} {du} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{4}}{u}^{−\mathrm{12}} +\frac{\mathrm{6}}{\mathrm{13}}{u}^{−\mathrm{13}} −\frac{\mathrm{3}}{\mathrm{14}}{u}^{−\mathrm{14}} +{c} \\ $$$$=\frac{\mathrm{6}}{\mathrm{13}{u}^{\mathrm{13}} }−\frac{\mathrm{3}}{\mathrm{14}{u}^{\mathrm{14}} }−\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{12}} }+{c} \\ $$$$=\frac{\mathrm{6}}{\mathrm{13}\left(\mathrm{1}+{t}\right)^{\mathrm{13}} }−\frac{\mathrm{3}}{\mathrm{14}\left(\mathrm{1}−{t}\right)^{\mathrm{14}} }−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}−{t}\right)^{\mathrm{12}} }+{c} \\ $$
