Question Number 139076 by bramlexs22 last updated on 22/Apr/21
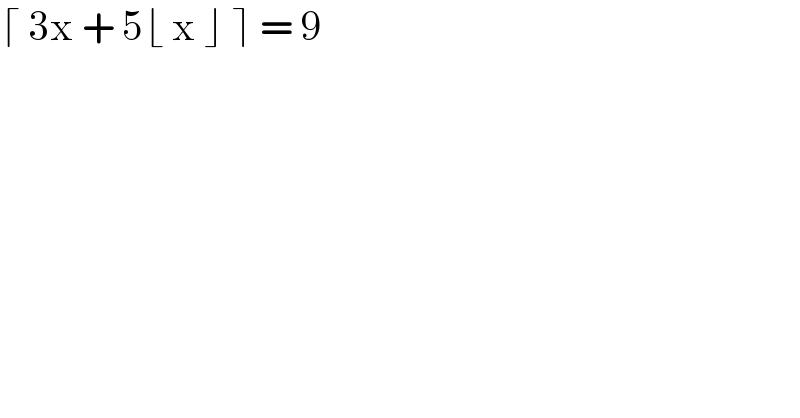
$$\lceil\:\mathrm{3x}\:+\:\mathrm{5}\lfloor\:\mathrm{x}\:\rfloor\:\rceil\:=\:\mathrm{9} \\ $$
Answered by mathmax by abdo last updated on 22/Apr/21
![⇒[3x]+5[x]=9 let [x]=n ⇒n≤x<n+1 ⇒3n≤3x<3n+3 if 3n≤3x<3n+1 ⇒[3x]=3n and e⇒3n+5n=9 ⇒8n=9 impossible if 3n+1≤3x<3n+2 ⇒[3x]=3n+1 and e⇒3n+1+5n=9 ⇒8n=8 ⇒n=1 ⇒4≤3x<5 ⇒(4/3)≤x<(5/3) if 3n+2≤3x<3n+3 ⇒[3x]=3n+2 and e⇒3n+2+5n=9 ⇒ 8n=7 impossible so the set of solution is S=[(4/3),(5/3)[](https://www.tinkutara.com/question/Q139077.png)
$$\Rightarrow\left[\mathrm{3x}\right]+\mathrm{5}\left[\mathrm{x}\right]=\mathrm{9}\:\:\:\mathrm{let}\:\left[\mathrm{x}\right]=\mathrm{n}\:\Rightarrow\mathrm{n}\leqslant\mathrm{x}<\mathrm{n}+\mathrm{1}\:\Rightarrow\mathrm{3n}\leqslant\mathrm{3x}<\mathrm{3n}+\mathrm{3} \\ $$$$\mathrm{if}\:\mathrm{3n}\leqslant\mathrm{3x}<\mathrm{3n}+\mathrm{1}\:\Rightarrow\left[\mathrm{3x}\right]=\mathrm{3n}\:\:\mathrm{and}\:\mathrm{e}\Rightarrow\mathrm{3n}+\mathrm{5n}=\mathrm{9}\:\Rightarrow\mathrm{8n}=\mathrm{9}\:\:\mathrm{impossible} \\ $$$$\mathrm{if}\:\mathrm{3n}+\mathrm{1}\leqslant\mathrm{3x}<\mathrm{3n}+\mathrm{2}\:\Rightarrow\left[\mathrm{3x}\right]=\mathrm{3n}+\mathrm{1}\:\:\mathrm{and}\:\mathrm{e}\Rightarrow\mathrm{3n}+\mathrm{1}+\mathrm{5n}=\mathrm{9}\:\Rightarrow\mathrm{8n}=\mathrm{8} \\ $$$$\Rightarrow\mathrm{n}=\mathrm{1}\:\Rightarrow\mathrm{4}\leqslant\mathrm{3x}<\mathrm{5}\:\Rightarrow\frac{\mathrm{4}}{\mathrm{3}}\leqslant\mathrm{x}<\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{if}\:\:\mathrm{3n}+\mathrm{2}\leqslant\mathrm{3x}<\mathrm{3n}+\mathrm{3}\:\Rightarrow\left[\mathrm{3x}\right]=\mathrm{3n}+\mathrm{2}\:\mathrm{and}\:\mathrm{e}\Rightarrow\mathrm{3n}+\mathrm{2}+\mathrm{5n}=\mathrm{9}\:\Rightarrow \\ $$$$\mathrm{8n}=\mathrm{7}\:\:\mathrm{impossible}\:\mathrm{so}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{S}=\left[\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{5}}{\mathrm{3}}\left[\right.\right. \\ $$
Answered by mr W last updated on 22/Apr/21
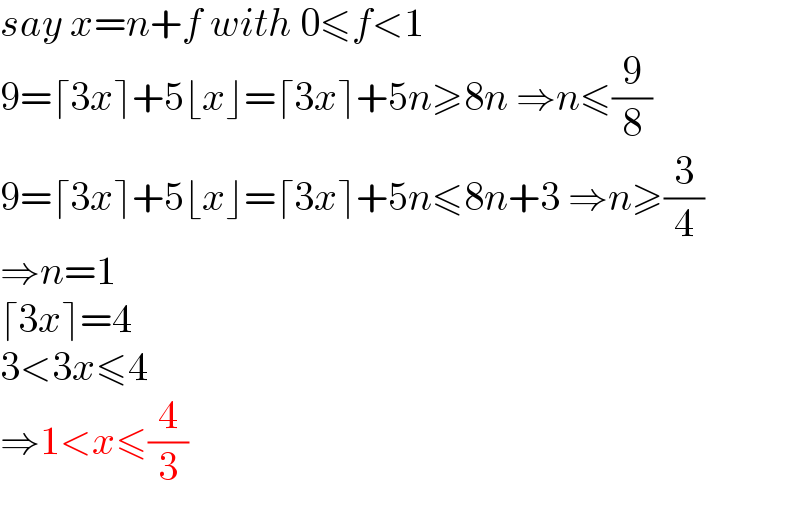
$${say}\:{x}={n}+{f}\:{with}\:\mathrm{0}\leqslant{f}<\mathrm{1} \\ $$$$\mathrm{9}=\lceil\mathrm{3}{x}\rceil+\mathrm{5}\lfloor{x}\rfloor=\lceil\mathrm{3}{x}\rceil+\mathrm{5}{n}\geqslant\mathrm{8}{n}\:\Rightarrow{n}\leqslant\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\mathrm{9}=\lceil\mathrm{3}{x}\rceil+\mathrm{5}\lfloor{x}\rfloor=\lceil\mathrm{3}{x}\rceil+\mathrm{5}{n}\leqslant\mathrm{8}{n}+\mathrm{3}\:\Rightarrow{n}\geqslant\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{n}=\mathrm{1} \\ $$$$\lceil\mathrm{3}{x}\rceil=\mathrm{4} \\ $$$$\mathrm{3}<\mathrm{3}{x}\leqslant\mathrm{4} \\ $$$$\Rightarrow\mathrm{1}<{x}\leqslant\frac{\mathrm{4}}{\mathrm{3}} \\ $$
