Question Number 74723 by necxxx last updated on 29/Nov/19
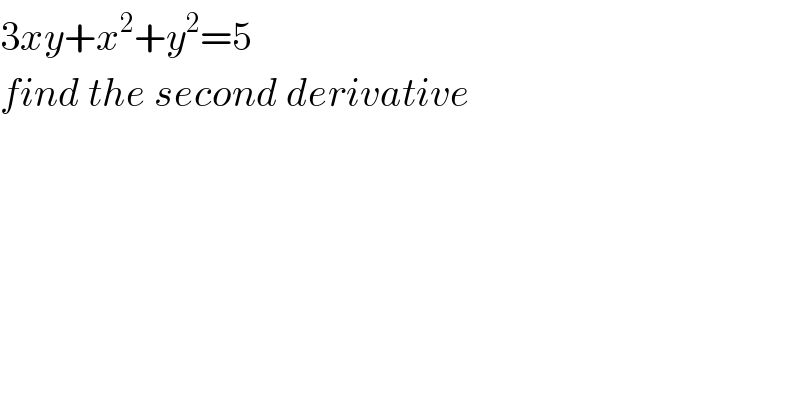
$$\mathrm{3}{xy}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{5} \\ $$$${find}\:{the}\:{second}\:{derivative} \\ $$
Commented by mathmax by abdo last updated on 29/Nov/19
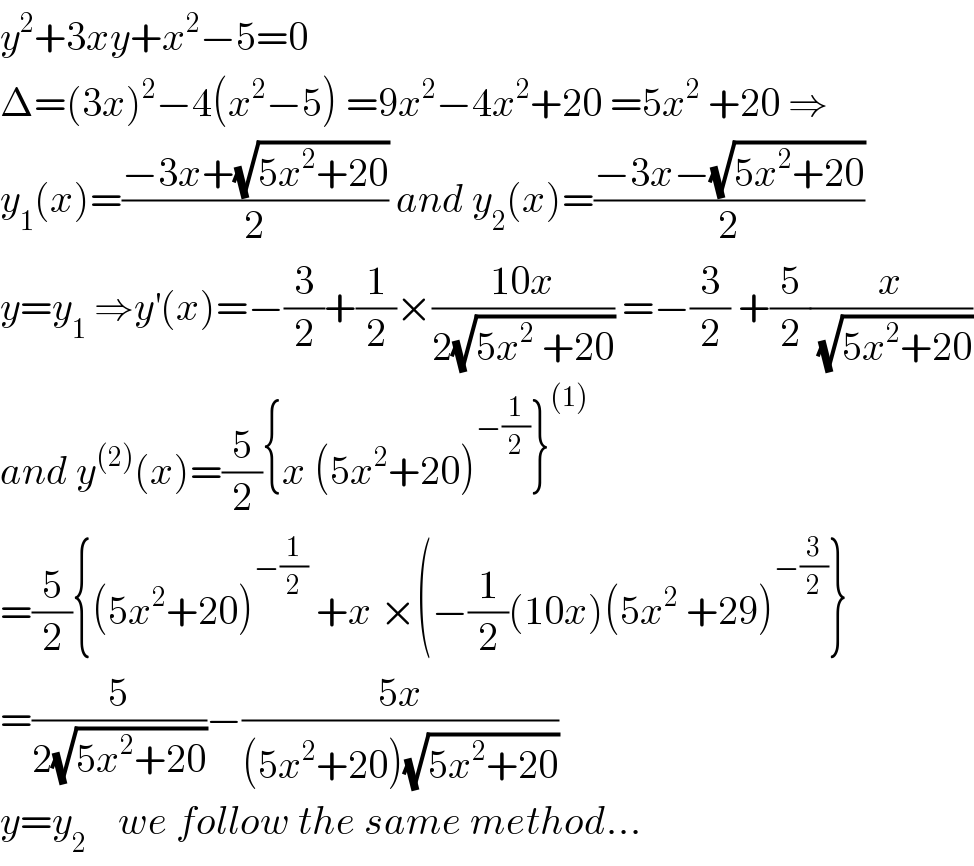
$${y}^{\mathrm{2}} +\mathrm{3}{xy}+{x}^{\mathrm{2}} −\mathrm{5}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{3}{x}\right)^{\mathrm{2}} −\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{5}\right)\:=\mathrm{9}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{20}\:=\mathrm{5}{x}^{\mathrm{2}} \:+\mathrm{20}\:\Rightarrow \\ $$$${y}_{\mathrm{1}} \left({x}\right)=\frac{−\mathrm{3}{x}+\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}}}{\mathrm{2}}\:{and}\:{y}_{\mathrm{2}} \left({x}\right)=\frac{−\mathrm{3}{x}−\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}}}{\mathrm{2}} \\ $$$${y}={y}_{\mathrm{1}} \:\Rightarrow{y}^{'} \left({x}\right)=−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{10}{x}}{\mathrm{2}\sqrt{\mathrm{5}{x}^{\mathrm{2}} \:+\mathrm{20}}}\:=−\frac{\mathrm{3}}{\mathrm{2}}\:+\frac{\mathrm{5}}{\mathrm{2}}\frac{{x}}{\:\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}}} \\ $$$${and}\:{y}^{\left(\mathrm{2}\right)} \left({x}\right)=\frac{\mathrm{5}}{\mathrm{2}}\left\{{x}\:\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\left\{\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:+{x}\:×\left(−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{10}{x}\right)\left(\mathrm{5}{x}^{\mathrm{2}} \:+\mathrm{29}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \right\}\right. \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}}}−\frac{\mathrm{5}{x}}{\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}\right)\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}}} \\ $$$${y}={y}_{\mathrm{2}} \:\:\:\:{we}\:{follow}\:{the}\:{same}\:{method}… \\ $$
Answered by Tanmay chaudhury last updated on 29/Nov/19
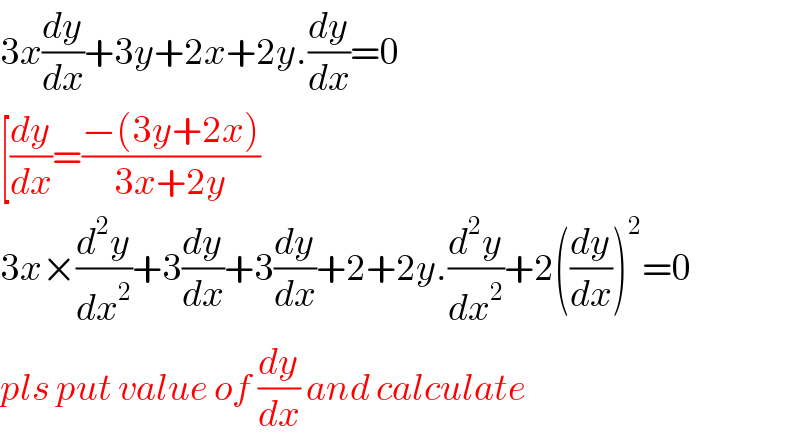
$$\mathrm{3}{x}\frac{{dy}}{{dx}}+\mathrm{3}{y}+\mathrm{2}{x}+\mathrm{2}{y}.\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\left[\frac{{dy}}{{dx}}=\frac{−\left(\mathrm{3}{y}+\mathrm{2}{x}\right)}{\mathrm{3}{x}+\mathrm{2}{y}}\right. \\ $$$$\mathrm{3}{x}×\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{3}\frac{{dy}}{{dx}}+\mathrm{3}\frac{{dy}}{{dx}}+\mathrm{2}+\mathrm{2}{y}.\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{2}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${pls}\:{put}\:{value}\:{of}\:\frac{{dy}}{{dx}}\:{and}\:{calculate} \\ $$
Commented by necxxx last updated on 29/Nov/19
$${Thank}\:{you}\:{so}\:{much}\:{sir}. \\ $$
