Question Number 7552 by Master Moon last updated on 03/Sep/16

$$\sqrt{\mathrm{4}}+\mathrm{5}\:= \\ $$
Answered by FilupSmith last updated on 03/Sep/16

$$\sqrt{\mathrm{4}}=\pm\mathrm{2} \\ $$$$\therefore\sqrt{\mathrm{4}}+\mathrm{5}=\mathrm{5}\pm\mathrm{2}=\mathrm{3},\:\mathrm{7} \\ $$
Commented by Rasheed Soomro last updated on 03/Sep/16
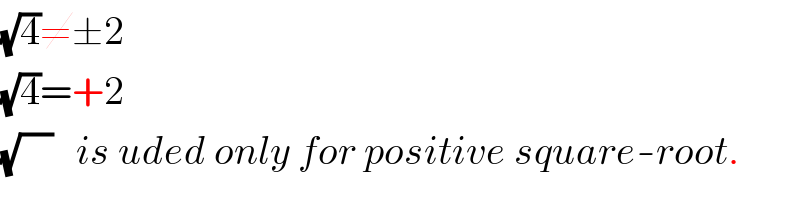
$$\sqrt{\mathrm{4}}\neq\pm\mathrm{2} \\ $$$$\sqrt{\mathrm{4}}=+\mathrm{2} \\ $$$$\sqrt{\:\:\:\:}\:\:\:{is}\:{uded}\:{only}\:{for}\:{positive}\:{square}-{root}. \\ $$
Commented by FilupSmith last updated on 03/Sep/16

$$\mathrm{4}=\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{4}=\left(−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{doesn}'\mathrm{t}\:\sqrt{\mathrm{4}}=\pm\mathrm{2}? \\ $$
Commented by Rasheed Soomro last updated on 03/Sep/16

$$\mathrm{4}\:{has}\:{no}\:{doubt}\:{two}\:{square}\:{roots} \\ $$$${but}\:{the}\:{symbol}\:\sqrt{\:\:\:}\:\:{is}\:{used}\:{for}\:+{ve} \\ $$$${square}\:{root}\:{only}.\:{For}\:−{ve}\:{square}\:{root} \\ $$$${symbol}\:\:−\sqrt{\:\:\:\:}\:\:\:\:{is}\:{used}.{For}\:{both}\:{roots}\:\: \\ $$$$\pm\sqrt{\:\:\:\:\:}\:\:{is}\:{used}.\:{I}\:{think}. \\ $$$${So}\: \\ $$$$\:\:\:\:\:\:\:\sqrt{\mathrm{4}}\:=\mathrm{2} \\ $$$$\:\:\:\:−\sqrt{\mathrm{4}}\:=−\mathrm{2} \\ $$$$\:\:\:\pm\sqrt{\mathrm{4}}\:=\pm\mathrm{2} \\ $$
