Question Number 537 by kth last updated on 25/Jan/15
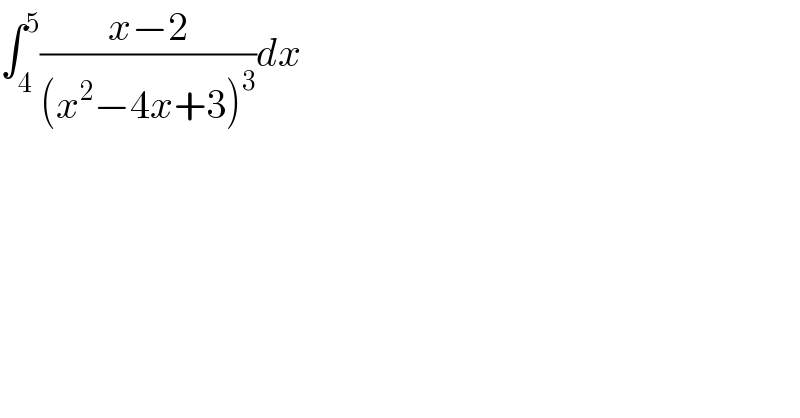
$$\int_{\mathrm{4}} ^{\mathrm{5}} \frac{{x}−\mathrm{2}}{\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right)^{\mathrm{3}} }{dx} \\ $$
Answered by Vishal last updated on 25/Jan/15
![let x^2 −4x+3 = t then (x−2) dx = (dt/2) ⇒ ∫_t_1 ^t_2 (dt/(2(t)^3 )) = (1/2)∫_3 ^8 t^(−3) dt = ((−1)/4)[(1/t^2 )]_3 ^8 ⇒ ((−1)/4) [(1/(64)) − (1/9)] = ((−1)/4) (((−55)/(576))) = ((55)/(2304))](https://www.tinkutara.com/question/Q539.png)
$${let}\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\:=\:{t}\:{then}\:\left({x}−\mathrm{2}\right)\:{dx}\:=\:\frac{{dt}}{\mathrm{2}} \\ $$$$\Rightarrow\:\int_{{t}_{\mathrm{1}} } ^{{t}_{\mathrm{2}} } \frac{{dt}}{\mathrm{2}\left({t}\right)^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{8}} \:{t}^{−\mathrm{3}} {dt}\:=\:\frac{−\mathrm{1}}{\mathrm{4}}\left[\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right]_{\mathrm{3}} ^{\mathrm{8}} \\ $$$$\Rightarrow\:\frac{−\mathrm{1}}{\mathrm{4}}\:\left[\frac{\mathrm{1}}{\mathrm{64}}\:−\:\frac{\mathrm{1}}{\mathrm{9}}\right]\:=\:\frac{−\mathrm{1}}{\mathrm{4}}\:\left(\frac{−\mathrm{55}}{\mathrm{576}}\right)\:=\:\frac{\mathrm{55}}{\mathrm{2304}} \\ $$
