Menu Close

4-x-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 136948 by leena12345 last updated on 28/Mar/21
∫((√(4+x^2 ))/x)dx
$$\int\frac{\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{{x}}{dx} \\ $$
Answered by Olaf last updated on 28/Mar/21
F(x) = ∫((√(4+x^2 ))/x) dx F(u) =^(x=2shu) ∫((√(4+4sh^2 u))/(2shu)) 2chudu F(u) = ∫((2chu)/(2shu)) 2chudu F(u) = 2∫((ch^2 u)/(shu)) du F(u) = 2∫((sh^2 u+1)/(shu)) du F(u) = 2∫(shu+(1/(shu))) du F(u) = 2∫(shu−((2e^u )/(1−e^(2u) ))) du F(u) = 2[chu−2argth(e^u )] F(u) = 2[(√(sh^2 u+1))−2×(1/2)ln∣((1+e^u )/(1−e^u ))∣] F(u) = 2[(√(sh^2 u+1))−2×(1/2)ln∣((1+shu+chu)/(1−shu−chu))∣] F(x) = (√(x^2 +4))−2ln∣((1+(x/2)+(√((x^2 /4)+1)))/(1−(x/2)−(√((x^2 /4)+1))))∣ (+C) F(x) = (√(x^2 +4))−2ln∣((2+x+(√(x^2 +4)))/(2−x−(√(x^2 +4))))∣ (+C)
$$\mathrm{F}\left({x}\right)\:=\:\int\frac{\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{{x}}\:{dx} \\ $$$$\mathrm{F}\left({u}\right)\:\overset{{x}=\mathrm{2sh}{u}} {=}\:\:\:\:\int\frac{\sqrt{\mathrm{4}+\mathrm{4sh}^{\mathrm{2}} {u}}}{\mathrm{2sh}{u}}\:\mathrm{2ch}{udu} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\int\frac{\mathrm{2ch}{u}}{\mathrm{2sh}{u}}\:\mathrm{2ch}{udu} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\mathrm{2}\int\frac{\mathrm{ch}^{\mathrm{2}} {u}}{\mathrm{sh}{u}}\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\mathrm{2}\int\frac{\mathrm{sh}^{\mathrm{2}} {u}+\mathrm{1}}{\mathrm{sh}{u}}\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\mathrm{2}\int\left(\mathrm{sh}{u}+\frac{\mathrm{1}}{\mathrm{sh}{u}}\right)\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\mathrm{2}\int\left(\mathrm{sh}{u}−\frac{\mathrm{2}{e}^{{u}} }{\mathrm{1}−{e}^{\mathrm{2}{u}} }\right)\:{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\mathrm{2}\left[\mathrm{ch}{u}−\mathrm{2argth}\left({e}^{{u}} \right)\right] \\ $$$$\mathrm{F}\left({u}\right)\:=\:\mathrm{2}\left[\sqrt{\mathrm{sh}^{\mathrm{2}} {u}+\mathrm{1}}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+{e}^{{u}} }{\mathrm{1}−{e}^{{u}} }\mid\right] \\ $$$$\mathrm{F}\left({u}\right)\:=\:\mathrm{2}\left[\sqrt{\mathrm{sh}^{\mathrm{2}} {u}+\mathrm{1}}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{shu}+\mathrm{ch}{u}}{\mathrm{1}−\mathrm{sh}{u}−\mathrm{ch}{u}}\mid\right] \\ $$$$\mathrm{F}\left({x}\right)\:=\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}−\mathrm{2ln}\mid\frac{\mathrm{1}+\frac{{x}}{\mathrm{2}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}}}{\mathrm{1}−\frac{{x}}{\mathrm{2}}−\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}}}\mid\:\left(+\mathrm{C}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}−\mathrm{2ln}\mid\frac{\mathrm{2}+{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}−{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\mid\:\left(+\mathrm{C}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 28/Mar/21
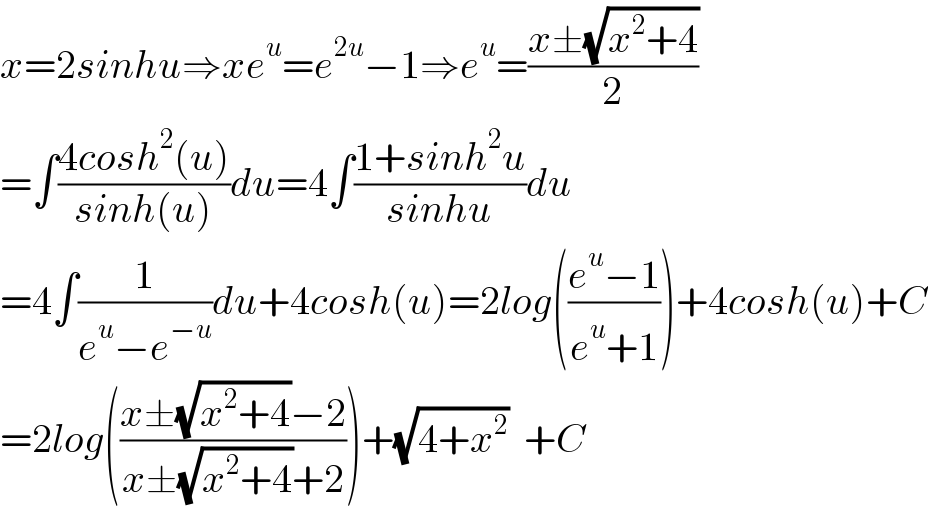
x=2sinhu⇒xe^u =e^(2u) −1⇒e^u =((x±(√(x^2 +4)))/2) =∫((4cosh^2 (u))/(sinh(u)))du=4∫((1+sinh^2 u)/(sinhu))du =4∫(1/(e^u −e^(−u) ))du+4cosh(u)=2log(((e^u −1)/(e^u +1)))+4cosh(u)+C =2log(((x±(√(x^2 +4))−2)/(x±(√(x^2 +4))+2)))+(√(4+x^2 )) +C
$${x}=\mathrm{2}{sinhu}\Rightarrow{xe}^{{u}} ={e}^{\mathrm{2}{u}} −\mathrm{1}\Rightarrow{e}^{{u}} =\frac{{x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$$=\int\frac{\mathrm{4}{cosh}^{\mathrm{2}} \left({u}\right)}{{sinh}\left({u}\right)}{du}=\mathrm{4}\int\frac{\mathrm{1}+{sinh}^{\mathrm{2}} {u}}{{sinhu}}{du} \\ $$$$=\mathrm{4}\int\frac{\mathrm{1}}{{e}^{{u}} −{e}^{−{u}} }{du}+\mathrm{4}{cosh}\left({u}\right)=\mathrm{2}{log}\left(\frac{{e}^{{u}} −\mathrm{1}}{{e}^{{u}} +\mathrm{1}}\right)+\mathrm{4}{cosh}\left({u}\right)+{C} \\ $$$$=\mathrm{2}{log}\left(\frac{{x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}−\mathrm{2}}{{x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}+\mathrm{2}}\right)+\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:\:+{C} \\ $$
Answered by mathmax by abdo last updated on 28/Mar/21
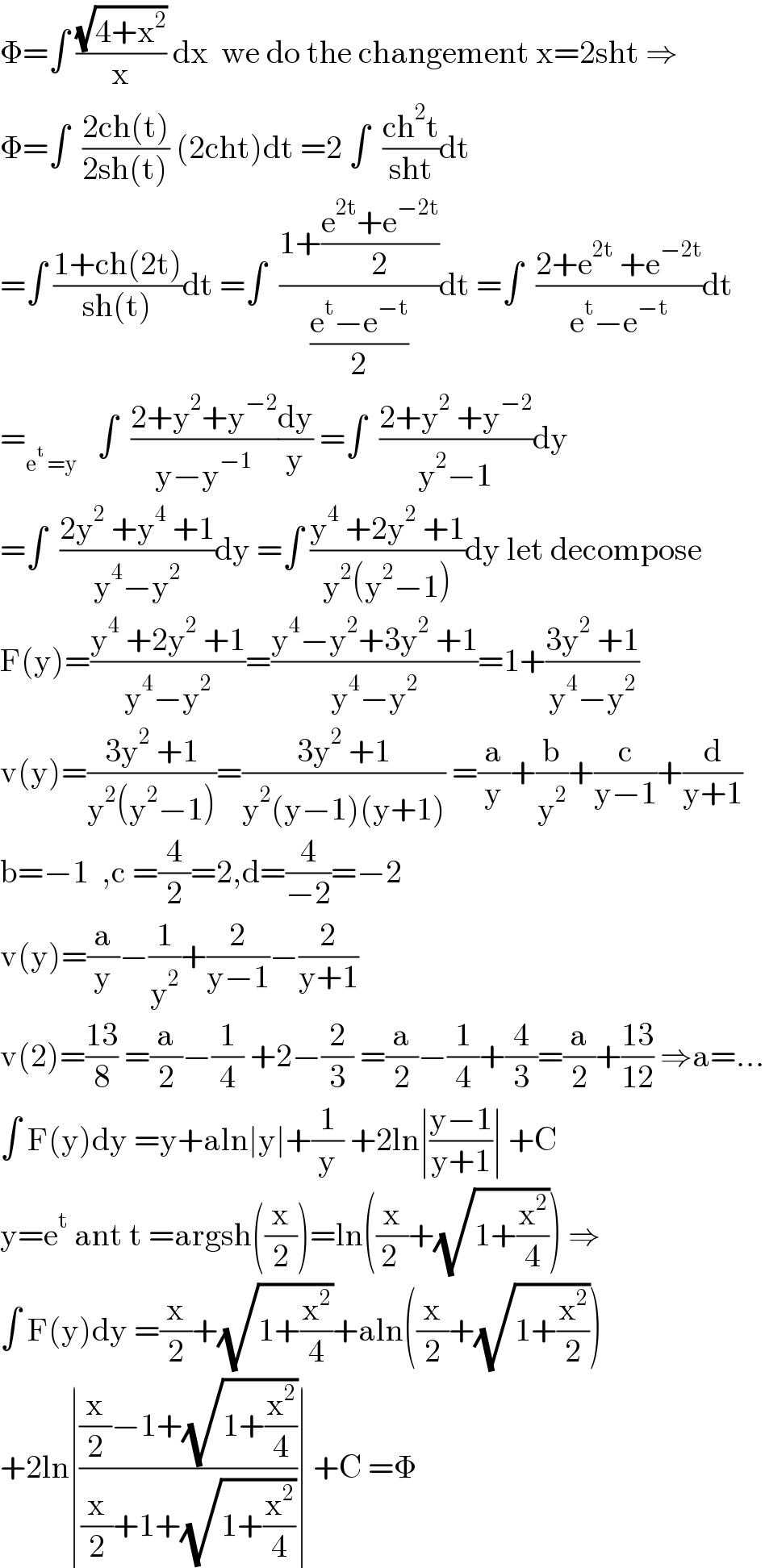
Φ=∫ ((√(4+x^2 ))/x) dx we do the changement x=2sht ⇒ Φ=∫ ((2ch(t))/(2sh(t))) (2cht)dt =2 ∫ ((ch^2 t)/(sht))dt =∫ ((1+ch(2t))/(sh(t)))dt =∫ ((1+((e^(2t) +e^(−2t) )/2))/((e^t −e^(−t) )/2))dt =∫ ((2+e^(2t) +e^(−2t) )/(e^t −e^(−t) ))dt =_(e^t =y) ∫ ((2+y^2 +y^(−2) )/(y−y^(−1) ))(dy/y) =∫ ((2+y^2 +y^(−2) )/(y^2 −1))dy =∫ ((2y^2 +y^4 +1)/(y^4 −y^2 ))dy =∫ ((y^4 +2y^2 +1)/(y^2 (y^2 −1)))dy let decompose F(y)=((y^4 +2y^2 +1)/(y^4 −y^2 ))=((y^4 −y^2 +3y^2 +1)/(y^4 −y^2 ))=1+((3y^2 +1)/(y^4 −y^2 )) v(y)=((3y^2 +1)/(y^2 (y^2 −1)))=((3y^2 +1)/(y^2 (y−1)(y+1))) =(a/y)+(b/y^2 )+(c/(y−1))+(d/(y+1)) b=−1 ,c =(4/2)=2,d=(4/(−2))=−2 v(y)=(a/y)−(1/y^2 )+(2/(y−1))−(2/(y+1)) v(2)=((13)/8) =(a/2)−(1/4) +2−(2/3) =(a/2)−(1/4)+(4/3)=(a/2)+((13)/(12)) ⇒a=... ∫ F(y)dy =y+aln∣y∣+(1/y) +2ln∣((y−1)/(y+1))∣ +C y=e^t ant t =argsh((x/2))=ln((x/(2 ))+(√(1+(x^2 /4)))) ⇒ ∫ F(y)dy =(x/2)+(√(1+(x^2 /4)))+aln((x/2)+(√(1+(x^2 /2)))) +2ln∣(((x/2)−1+(√(1+(x^2 /4))))/((x/2)+1+(√(1+(x^2 /4)))))∣ +C =Φ
$$\Phi=\int\:\frac{\sqrt{\mathrm{4}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\:\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{2sht}\:\Rightarrow \\ $$$$\Phi=\int\:\:\frac{\mathrm{2ch}\left(\mathrm{t}\right)}{\mathrm{2sh}\left(\mathrm{t}\right)}\:\left(\mathrm{2cht}\right)\mathrm{dt}\:=\mathrm{2}\:\int\:\:\frac{\mathrm{ch}^{\mathrm{2}} \mathrm{t}}{\mathrm{sht}}\mathrm{dt} \\ $$$$=\int\:\frac{\mathrm{1}+\mathrm{ch}\left(\mathrm{2t}\right)}{\mathrm{sh}\left(\mathrm{t}\right)}\mathrm{dt}\:=\int\:\:\frac{\mathrm{1}+\frac{\mathrm{e}^{\mathrm{2t}} +\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}}{\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}\mathrm{dt}\:=\int\:\:\frac{\mathrm{2}+\mathrm{e}^{\mathrm{2t}} \:+\mathrm{e}^{−\mathrm{2t}} }{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }\mathrm{dt} \\ $$$$=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{y}} \:\:\:\int\:\:\frac{\mathrm{2}+\mathrm{y}^{\mathrm{2}} +\mathrm{y}^{−\mathrm{2}} }{\mathrm{y}−\mathrm{y}^{−\mathrm{1}} }\frac{\mathrm{dy}}{\mathrm{y}}\:=\int\:\:\frac{\mathrm{2}+\mathrm{y}^{\mathrm{2}} \:+\mathrm{y}^{−\mathrm{2}} }{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}\mathrm{dy} \\ $$$$=\int\:\:\frac{\mathrm{2y}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{4}} \:+\mathrm{1}}{\mathrm{y}^{\mathrm{4}} −\mathrm{y}^{\mathrm{2}} }\mathrm{dy}\:=\int\:\frac{\mathrm{y}^{\mathrm{4}} \:+\mathrm{2y}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{y}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)}\mathrm{dy}\:\mathrm{let}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{y}\right)=\frac{\mathrm{y}^{\mathrm{4}} \:+\mathrm{2y}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{y}^{\mathrm{4}} −\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{y}^{\mathrm{4}} −\mathrm{y}^{\mathrm{2}} +\mathrm{3y}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{y}^{\mathrm{4}} −\mathrm{y}^{\mathrm{2}} }=\mathrm{1}+\frac{\mathrm{3y}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{y}^{\mathrm{4}} −\mathrm{y}^{\mathrm{2}} } \\ $$$$\mathrm{v}\left(\mathrm{y}\right)=\frac{\mathrm{3y}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{y}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{\mathrm{3y}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{y}^{\mathrm{2}} \left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}+\mathrm{1}\right)}\:=\frac{\mathrm{a}}{\mathrm{y}}+\frac{\mathrm{b}}{\mathrm{y}^{\mathrm{2}} }+\frac{\mathrm{c}}{\mathrm{y}−\mathrm{1}}+\frac{\mathrm{d}}{\mathrm{y}+\mathrm{1}} \\ $$$$\mathrm{b}=−\mathrm{1}\:\:,\mathrm{c}\:=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2},\mathrm{d}=\frac{\mathrm{4}}{−\mathrm{2}}=−\mathrm{2} \\ $$$$\mathrm{v}\left(\mathrm{y}\right)=\frac{\mathrm{a}}{\mathrm{y}}−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{y}−\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{y}+\mathrm{1}} \\ $$$$\mathrm{v}\left(\mathrm{2}\right)=\frac{\mathrm{13}}{\mathrm{8}}\:=\frac{\mathrm{a}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\:+\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}\:=\frac{\mathrm{a}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{a}}{\mathrm{2}}+\frac{\mathrm{13}}{\mathrm{12}}\:\Rightarrow\mathrm{a}=… \\ $$$$\int\:\mathrm{F}\left(\mathrm{y}\right)\mathrm{dy}\:=\mathrm{y}+\mathrm{aln}\mid\mathrm{y}\mid+\frac{\mathrm{1}}{\mathrm{y}}\:+\mathrm{2ln}\mid\frac{\mathrm{y}−\mathrm{1}}{\mathrm{y}+\mathrm{1}}\mid\:+\mathrm{C} \\ $$$$\mathrm{y}=\mathrm{e}^{\mathrm{t}} \:\mathrm{ant}\:\mathrm{t}\:=\mathrm{argsh}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{ln}\left(\frac{\mathrm{x}}{\mathrm{2}\:}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}\right)\:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{y}\right)\mathrm{dy}\:=\frac{\mathrm{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}+\mathrm{aln}\left(\frac{\mathrm{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}}\right) \\ $$$$+\mathrm{2ln}\mid\frac{\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}}{\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}}\mid\:+\mathrm{C}\:=\Phi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *