4-x-x-1-5-4-6x-x-1-5-1-x-1-x-2-

Question Number 11515 by @ANTARES_VY last updated on 27/Mar/17

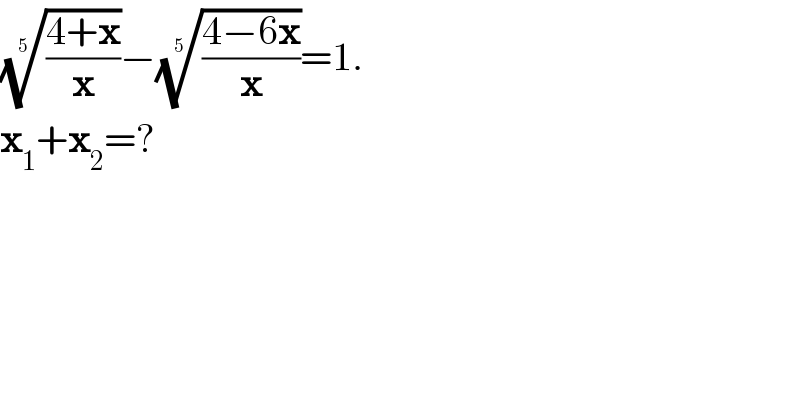
$$\sqrt[{\mathrm{5}}]{\frac{\mathrm{4}+\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}}}−\sqrt[{\mathrm{5}}]{\frac{\mathrm{4}−\mathrm{6}\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}}}=\mathrm{1}. \\ $$$$\boldsymbol{\mathrm{x}}_{\mathrm{1}} +\boldsymbol{\mathrm{x}}_{\mathrm{2}} =? \\ $$

Answered by ajfour last updated on 27/Mar/17

$$\mathrm{x}=\frac{\mathrm{4}}{\mathrm{15}} \\ $$

Commented by ajfour last updated on 27/Mar/17

(√((4+x)/x))+(√((4−6x)/x))=1 ....(i) let (√((4+x)/x))−(√((4−6x)/x))=a ...(ii) multiplying above two equations (((4+x)/x) )− (((4−6x)/x) )=a ⇒ 7=a adding (i) and (ii): 2(√((4+x)/x)) = a+1 = 8 (as a=7 ) ⇒ ((4+x)/x) =16 ⇒ 15x =4 x = (4/(15)) .

$$\sqrt{\frac{\mathrm{4}+\mathrm{x}}{\mathrm{x}}}+\sqrt{\frac{\mathrm{4}−\mathrm{6x}}{\mathrm{x}}}=\mathrm{1}\:\:\:….\left(\mathrm{i}\right) \\ $$$$\mathrm{let}\:\:\sqrt{\frac{\mathrm{4}+\mathrm{x}}{\mathrm{x}}}−\sqrt{\frac{\mathrm{4}−\mathrm{6x}}{\mathrm{x}}}=\mathrm{a}\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\mathrm{multiplying}\:\mathrm{above}\:\mathrm{two}\:\mathrm{equations} \\ $$$$\left(\frac{\mathrm{4}+\mathrm{x}}{\mathrm{x}}\:\right)−\:\left(\frac{\mathrm{4}−\mathrm{6x}}{\mathrm{x}}\:\right)=\mathrm{a} \\ $$$$\Rightarrow\:\:\mathrm{7}=\mathrm{a} \\ $$$$\mathrm{adding}\:\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right): \\ $$$$\mathrm{2}\sqrt{\frac{\mathrm{4}+\mathrm{x}}{\mathrm{x}}}\:=\:\mathrm{a}+\mathrm{1}\:=\:\mathrm{8}\:\:\left(\mathrm{as}\:\mathrm{a}=\mathrm{7}\:\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{4}+\mathrm{x}}{\mathrm{x}}\:=\mathrm{16} \\ $$$$\Rightarrow\:\mathrm{15x}\:=\mathrm{4} \\ $$$$\:\:\:\mathrm{x}\:=\:\frac{\mathrm{4}}{\mathrm{15}}\:\:. \\ $$

Commented by mrW1 last updated on 27/Mar/17

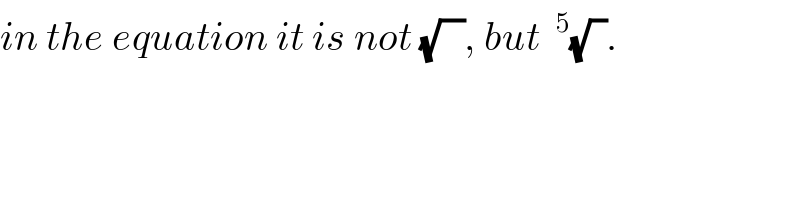
in the equation it is not (√( )), but ^5 (√( )).

$${in}\:{the}\:{equation}\:{it}\:{is}\:{not}\:\sqrt{\:\:\:},\:{but}\:\:^{\mathrm{5}} \sqrt{\:\:}. \\ $$

Commented by @ANTARES_VY last updated on 27/Mar/17

$$\boldsymbol{\mathrm{understand}}\:\:\boldsymbol{\mathrm{solved}} \\ $$

Commented by chux last updated on 27/Mar/17

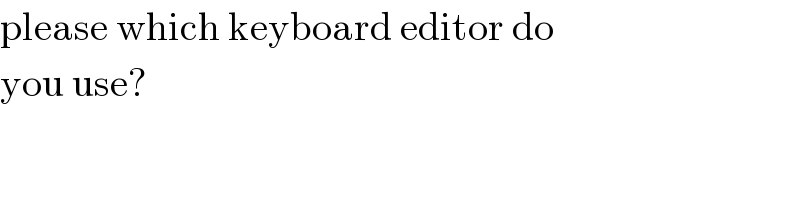
please which keyboard editor do you use?

$$\mathrm{please}\:\mathrm{which}\:\mathrm{keyboard}\:\mathrm{editor}\:\mathrm{do}\: \\ $$$$\mathrm{you}\:\mathrm{use}? \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17

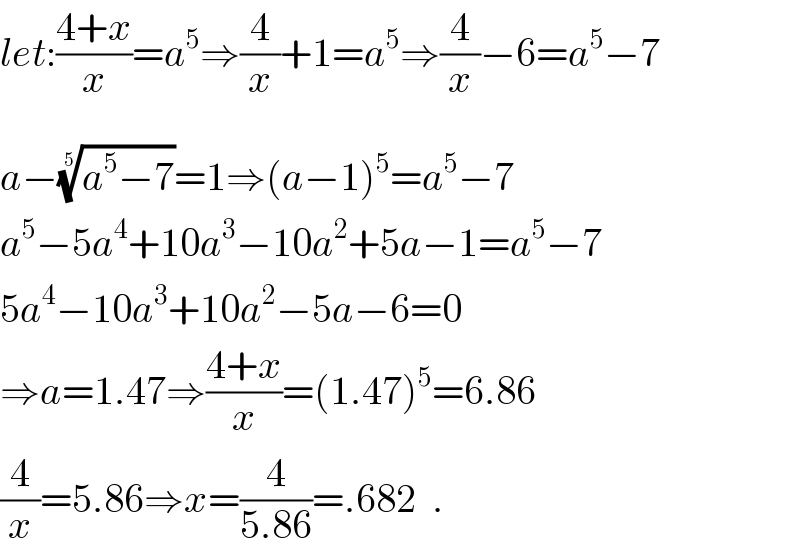
l_ et:((4+x)/x)=a^5 ⇒(4/x)+1=a^5 ⇒(4/x)−6=a^5 −7 a−((a^5 −7))^(1/5) =1⇒(a−1)^5 =a^5 −7 a^5 −5a^4 +10a^3 −10a^2 +5a−1=a^5 −7 5a^4 −10a^3 +10a^2 −5a−6=0 ⇒a=1.47⇒((4+x)/x)=(1.47)^5 =6.86 (4/x)=5.86⇒x=(4/(5.86))=.682 .

$$\underset{} {{l}et}:\frac{\mathrm{4}+{x}}{{x}}={a}^{\mathrm{5}} \Rightarrow\frac{\mathrm{4}}{{x}}+\mathrm{1}={a}^{\mathrm{5}} \Rightarrow\frac{\mathrm{4}}{{x}}−\mathrm{6}={a}^{\mathrm{5}} −\mathrm{7} \\ $$$${a}−\sqrt[{\mathrm{5}}]{{a}^{\mathrm{5}} −\mathrm{7}}=\mathrm{1}\Rightarrow\left({a}−\mathrm{1}\right)^{\mathrm{5}} ={a}^{\mathrm{5}} −\mathrm{7} \\ $$$${a}^{\mathrm{5}} −\mathrm{5}{a}^{\mathrm{4}} +\mathrm{10}{a}^{\mathrm{3}} −\mathrm{10}{a}^{\mathrm{2}} +\mathrm{5}{a}−\mathrm{1}={a}^{\mathrm{5}} −\mathrm{7} \\ $$$$\mathrm{5}{a}^{\mathrm{4}} −\mathrm{10}{a}^{\mathrm{3}} +\mathrm{10}{a}^{\mathrm{2}} −\mathrm{5}{a}−\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow{a}=\mathrm{1}.\mathrm{47}\Rightarrow\frac{\mathrm{4}+{x}}{{x}}=\left(\mathrm{1}.\mathrm{47}\right)^{\mathrm{5}} =\mathrm{6}.\mathrm{86} \\ $$$$\frac{\mathrm{4}}{{x}}=\mathrm{5}.\mathrm{86}\Rightarrow{x}=\frac{\mathrm{4}}{\mathrm{5}.\mathrm{86}}=.\mathrm{682}\:\:. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17