Question Number 136466 by aurpeyz last updated on 22/Mar/21
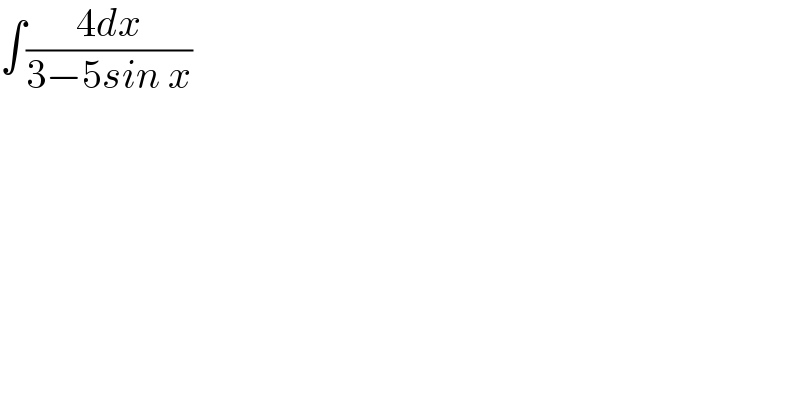
$$\int\frac{\mathrm{4}{dx}}{\mathrm{3}−\mathrm{5}{sin}\:{x}} \\ $$
Answered by mathmax by abdo last updated on 22/Mar/21

$$\Phi=\int\:\:\frac{\mathrm{4dx}}{\mathrm{3}−\mathrm{5sinx}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\Rightarrow \\ $$$$\Phi=\int\:\:\frac{\mathrm{4}}{\left(\mathrm{3}−\mathrm{5}\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\mathrm{8}\:\int\:\:\:\:\frac{\mathrm{dt}}{\mathrm{3}+\mathrm{3t}^{\mathrm{2}} −\mathrm{10t}} \\ $$$$=\mathrm{8}\int\:\:\frac{\mathrm{dt}}{\mathrm{3t}^{\mathrm{2}} −\mathrm{10t}\:+\mathrm{3}} \\ $$$$\Delta^{'} \:=\mathrm{25}−\mathrm{9}\:=\mathrm{16}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{4}}{\mathrm{3}}=\mathrm{3}\:\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$$\Phi=\mathrm{8}\int\:\:\:\:\frac{\mathrm{dt}}{\mathrm{3}\left(\mathrm{t}−\mathrm{3}\right)\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{3}}\right)}\:=\frac{\mathrm{8}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{8}}\int\:\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{3}}}\right)\mathrm{dt} \\ $$$$=\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{3}}{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{3}}}\mid+\mathrm{C}\:=\mathrm{ln}\mid\frac{\mathrm{3}\left(\mathrm{t}−\mathrm{3}\right)}{\mathrm{3t}−\mathrm{1}}\mid\:+\mathrm{C}\:=\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{3}}{\mathrm{3t}−\mathrm{1}}\mid\:+\mathrm{C} \\ $$$$\Phi=\mathrm{ln}\mid\frac{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{3}}{\mathrm{3tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{1}}\mid\:+\mathrm{C} \\ $$
