Question Number 142414 by mathdanisur last updated on 31/May/21
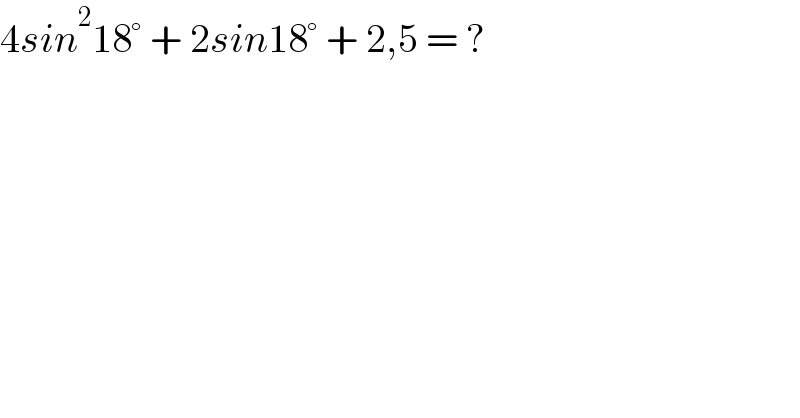
$$\mathrm{4}{sin}^{\mathrm{2}} \mathrm{18}°\:+\:\mathrm{2}{sin}\mathrm{18}°\:+\:\mathrm{2},\mathrm{5}\:=\:? \\ $$
Commented by som(math1967) last updated on 31/May/21

$$\mathrm{3}.\mathrm{5}\: \\ $$
Commented by mathdanisur last updated on 31/May/21
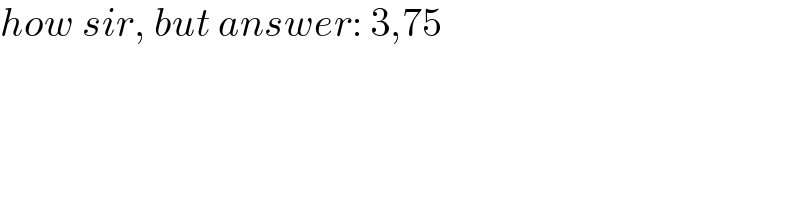
$${how}\:{sir},\:{but}\:{answer}:\:\mathrm{3},\mathrm{75} \\ $$
Answered by som(math1967) last updated on 31/May/21
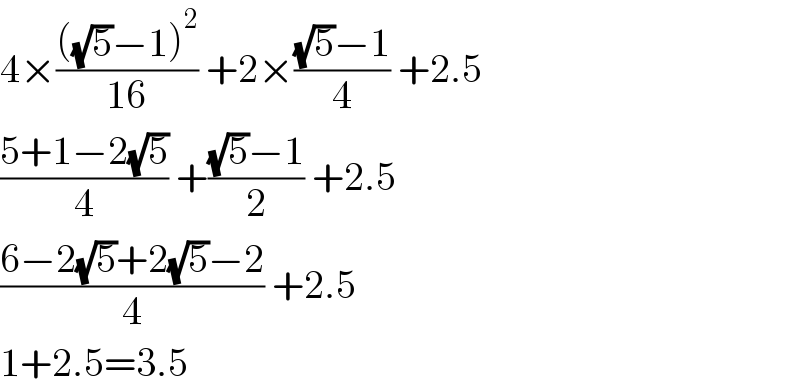
$$\mathrm{4}×\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{16}}\:+\mathrm{2}×\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:+\mathrm{2}.\mathrm{5} \\ $$$$\frac{\mathrm{5}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\:+\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\:+\mathrm{2}.\mathrm{5} \\ $$$$\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{2}}{\mathrm{4}}\:+\mathrm{2}.\mathrm{5} \\ $$$$\mathrm{1}+\mathrm{2}.\mathrm{5}=\mathrm{3}.\mathrm{5} \\ $$
Commented by mathdanisur last updated on 31/May/21

$${cool}\:{Sir}\:{thanks} \\ $$
