Question Number 11501 by @ANTARES_VY last updated on 27/Mar/17
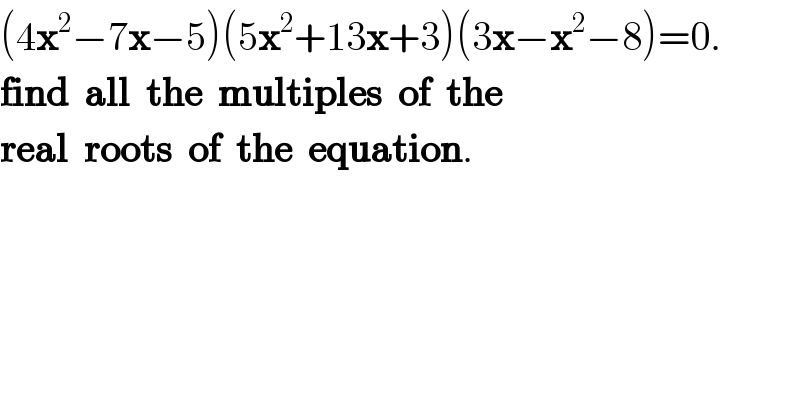
$$\left(\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{7}\boldsymbol{\mathrm{x}}−\mathrm{5}\right)\left(\mathrm{5}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{13}\boldsymbol{\mathrm{x}}+\mathrm{3}\right)\left(\mathrm{3}\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{8}\right)=\mathrm{0}. \\ $$$$\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{all}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{multiples}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{real}}\:\:\boldsymbol{\mathrm{roots}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{equation}}. \\ $$
Commented by mrW1 last updated on 27/Mar/17
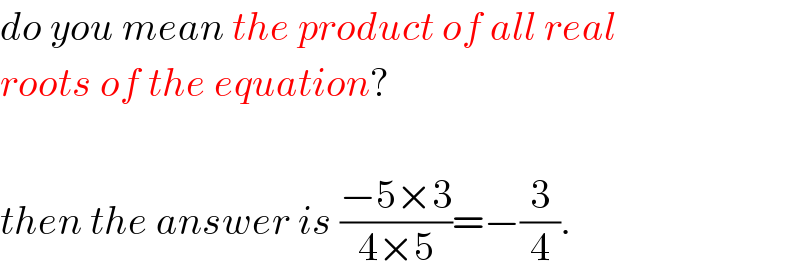
$${do}\:{you}\:{mean}\:{the}\:{product}\:{of}\:{all}\:{real} \\ $$$${roots}\:{of}\:{the}\:{equation}? \\ $$$$ \\ $$$${then}\:{the}\:{answer}\:{is}\:\frac{−\mathrm{5}×\mathrm{3}}{\mathrm{4}×\mathrm{5}}=−\frac{\mathrm{3}}{\mathrm{4}}. \\ $$
Answered by Joel576 last updated on 27/Mar/17

$$\bullet\:\mathrm{4}{x}^{\mathrm{2}} \:−\:\mathrm{7}{x}\:−\:\mathrm{5}\:=\:\mathrm{0} \\ $$$$\:\:\:\:{x}_{\mathrm{1},\mathrm{2}} \:=\:\frac{\mathrm{7}\:\pm\:\sqrt{\mathrm{49}\:−\:\left(\mathrm{4}.\mathrm{4}.−\mathrm{5}\right)}}{\mathrm{2}.\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{7}\:\pm\:\sqrt{\mathrm{129}}}{\mathrm{8}} \\ $$$$\:\:\:\:{x}_{\mathrm{1}} \:=\:\frac{\mathrm{7}\:+\:\sqrt{\mathrm{129}}}{\mathrm{8}} \\ $$$$\:\:\:\:{x}_{\mathrm{2}} \:=\:\frac{\mathrm{7}\:−\:\sqrt{\mathrm{129}}}{\mathrm{8}} \\ $$$$\bullet\:\mathrm{5}{x}^{\mathrm{2}} \:+\:\mathrm{13}{x}\:+\:\mathrm{3}\:=\:\mathrm{0} \\ $$$$\:\:\:\:{x}_{\mathrm{3},\mathrm{4}} \:=\:\frac{−\mathrm{13}\:\pm\:\sqrt{\mathrm{169}\:−\:\left(\mathrm{4}.\mathrm{5}.\mathrm{3}\right)}}{\mathrm{2}.\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{13}\:\pm\:\sqrt{\mathrm{109}}}{\mathrm{10}} \\ $$$$\:\:\:\:\:{x}_{\mathrm{3}} \:=\:\frac{−\mathrm{13}\:+\:\sqrt{\mathrm{109}}}{\mathrm{10}} \\ $$$$\:\:\:\:\:{x}_{\mathrm{4}} \:=\:\frac{−\mathrm{13}\:−\:\sqrt{\mathrm{109}}}{\mathrm{10}} \\ $$$$\bullet\:−{x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\:−\:\mathrm{8}\:=\:\mathrm{0} \\ $$$$\:\:\:\:{x}_{\mathrm{5},\mathrm{6}} \:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{\mathrm{9}\:−\:\left(\mathrm{4}.−\mathrm{1}.−\mathrm{8}\right)}}{\mathrm{2}.−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{−\mathrm{23}}}{−\mathrm{2}}\:\:\rightarrow\:\mathrm{imaginary} \\ $$$$\: \\ $$$$\left(\frac{\mathrm{7}\:+\:\sqrt{\mathrm{129}}}{\mathrm{8}}\:.\:\frac{\mathrm{7}\:−\:\sqrt{\mathrm{129}}}{\mathrm{8}}\right)\:\left(\frac{−\mathrm{13}\:+\:\sqrt{\mathrm{109}}}{\mathrm{10}}\:.\:\frac{−\mathrm{13}\:−\:\sqrt{\mathrm{109}}}{\mathrm{10}}\right) \\ $$$$=\:\left(\frac{\mathrm{49}\:−\:\mathrm{129}}{\mathrm{64}}\right)\left(\frac{\mathrm{169}\:−\:\mathrm{109}}{\mathrm{100}}\right) \\ $$$$=\:−\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by @ANTARES_VY last updated on 27/Mar/17

$$\boldsymbol{\mathrm{error}} \\ $$
Answered by sandy_suhendra last updated on 27/Mar/17

$$\mathrm{I}'\mathrm{ve}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake},\:\mathrm{so}\:\mathrm{I}\:\mathrm{corrected} \\ $$$$\mathrm{4x}^{\mathrm{2}} −\mathrm{7x}−\mathrm{5}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{x}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}\:} \mathrm{because}\:\mathrm{D}>\mathrm{0} \\ $$$$\mathrm{5x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{3}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{x}_{\mathrm{3}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{4}} \:\mathrm{because}\:\mathrm{D}>\mathrm{0}\:\:\:\:\:\: \\ $$$$\mathrm{3x}−\mathrm{x}^{\mathrm{2}} −\mathrm{8}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{imaginary}\:\mathrm{roots}\:\mathrm{because}\:\mathrm{D}<\mathrm{0} \\ $$$$\mathrm{so}\:\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{7x}−\mathrm{5}\right)\left(\mathrm{5x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{3}\right)=\mathrm{0}\:\mathrm{has}\:\mathrm{4}\:\mathrm{real}\:\mathrm{roots}\:\:\:\:\: \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{\mathrm{4}} =\mathrm{a} \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{\mathrm{3}} =\mathrm{b} \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} =\mathrm{c} \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{} =\mathrm{d} \\ $$$$\mathrm{constant}\:=\:\mathrm{e} \\ $$$$\mathrm{so}\:\mathrm{e}=−\mathrm{5}×\mathrm{3}=−\mathrm{15} \\ $$$$\:\:\:\:\:\mathrm{a}\:=\:\mathrm{4}×\mathrm{5}=\mathrm{20} \\ $$$$\mathrm{x}_{\mathrm{1}} .\mathrm{x}_{\mathrm{2}} .\mathrm{x}_{\mathrm{3}} .\mathrm{x}_{\mathrm{4}} =\frac{\mathrm{e}}{\mathrm{a}}=\frac{−\mathrm{15}}{\mathrm{20}}=−\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Answered by ajfour last updated on 27/Mar/17

$$\frac{\mathrm{3}}{\mathrm{4}}\mathrm{n}\:\:\mathrm{where}\:\mathrm{n}\:\mathrm{belongs}\:\mathrm{to}\:\mathrm{integers}. \\ $$
