Menu Close

5-1-x-1-x-6x-8-1-x-2-

Tinku Tara 0 Comments
Pin




Question Number 136494 by liberty last updated on 22/Mar/21
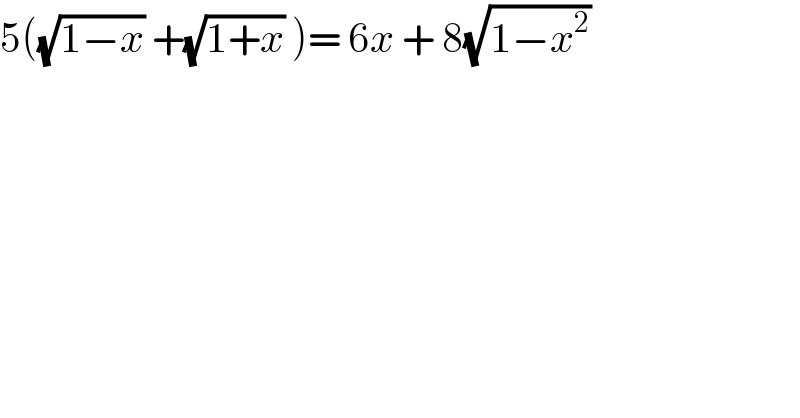
5((√(1−x)) +(√(1+x)) )= 6x + 8(√(1−x^2 ))
$$\mathrm{5}\left(\sqrt{\mathrm{1}−{x}}\:+\sqrt{\mathrm{1}+{x}}\:\right)=\:\mathrm{6}{x}\:+\:\mathrm{8}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\: \\ $$
Answered by MJS_new last updated on 22/Mar/21
I get 2 solutions x_1 =((24)/(25)) x_2 =cos ((π+2arcsin ((√2)/(10)))/3) ≈.415962301 the path is: let t=(√(1−x)) then transform, square and solve the 4^(th) degree for t, then test the 4 solutions you can also try with x=cos 2t but it′s not much easier...
$$\mathrm{I}\:\mathrm{get}\:\mathrm{2}\:\mathrm{solutions} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{24}}{\mathrm{25}} \\ $$$${x}_{\mathrm{2}} =\mathrm{cos}\:\frac{\pi+\mathrm{2arcsin}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{10}}}{\mathrm{3}}\:\approx.\mathrm{415962301} \\ $$$$\mathrm{the}\:\mathrm{path}\:\mathrm{is}:\:\mathrm{let}\:{t}=\sqrt{\mathrm{1}−{x}}\:\mathrm{then}\:\mathrm{transform}, \\ $$$$\mathrm{square}\:\mathrm{and}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{for}\:{t},\:\mathrm{then} \\ $$$$\mathrm{test}\:\mathrm{the}\:\mathrm{4}\:\mathrm{solutions} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{also}\:\mathrm{try}\:\mathrm{with}\:{x}=\mathrm{cos}\:\mathrm{2}{t}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{much} \\ $$$$\mathrm{easier}… \\ $$
Answered by mr W last updated on 22/Mar/21
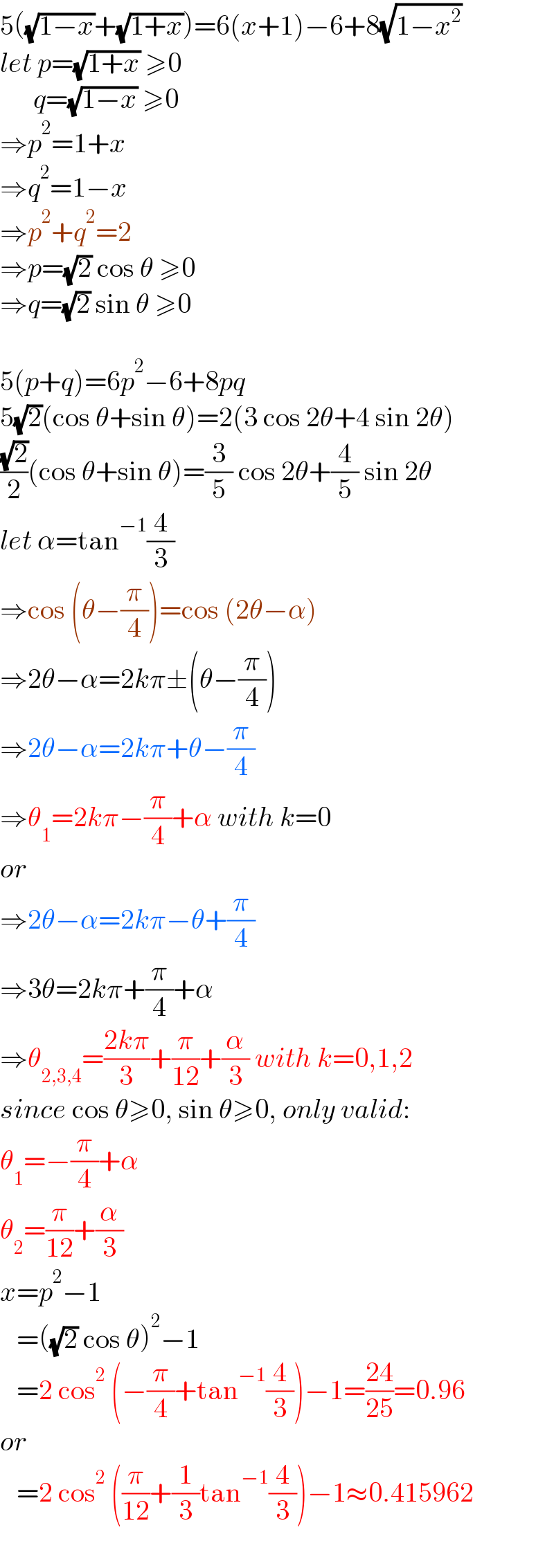
5((√(1−x))+(√(1+x)))=6(x+1)−6+8(√(1−x^2 )) let p=(√(1+x)) ≥0 q=(√(1−x)) ≥0 ⇒p^2 =1+x ⇒q^2 =1−x ⇒p^2 +q^2 =2 ⇒p=(√2) cos θ ≥0 ⇒q=(√2) sin θ ≥0 5(p+q)=6p^2 −6+8pq 5(√2)(cos θ+sin θ)=2(3 cos 2θ+4 sin 2θ) ((√2)/2)(cos θ+sin θ)=(3/5) cos 2θ+(4/5) sin 2θ let α=tan^(−1) (4/3) ⇒cos (θ−(π/4))=cos (2θ−α) ⇒2θ−α=2kπ±(θ−(π/4)) ⇒2θ−α=2kπ+θ−(π/4) ⇒θ_1 =2kπ−(π/4)+α with k=0 or ⇒2θ−α=2kπ−θ+(π/4) ⇒3θ=2kπ+(π/4)+α ⇒θ_(2,3,4) =((2kπ)/3)+(π/(12))+(α/3) with k=0,1,2 since cos θ≥0, sin θ≥0, only valid: θ_1 =−(π/4)+α θ_2 =(π/(12))+(α/3) x=p^2 −1 =((√2) cos θ)^2 −1 =2 cos^2 (−(π/4)+tan^(−1) (4/3))−1=((24)/(25))=0.96 or =2 cos^2 ((π/(12))+(1/3)tan^(−1) (4/3))−1≈0.415962
$$\mathrm{5}\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{1}+{x}}\right)=\mathrm{6}\left({x}+\mathrm{1}\right)−\mathrm{6}+\mathrm{8}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\: \\ $$$${let}\:{p}=\sqrt{\mathrm{1}+{x}}\:\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:{q}=\sqrt{\mathrm{1}−{x}}\:\geqslant\mathrm{0} \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\mathrm{1}+{x} \\ $$$$\Rightarrow{q}^{\mathrm{2}} =\mathrm{1}−{x} \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow{p}=\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta\:\geqslant\mathrm{0} \\ $$$$\Rightarrow{q}=\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta\:\geqslant\mathrm{0} \\ $$$$ \\ $$$$\mathrm{5}\left({p}+{q}\right)=\mathrm{6}{p}^{\mathrm{2}} −\mathrm{6}+\mathrm{8}{pq} \\ $$$$\mathrm{5}\sqrt{\mathrm{2}}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)=\mathrm{2}\left(\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{4}\:\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)=\frac{\mathrm{3}}{\mathrm{5}}\:\mathrm{cos}\:\mathrm{2}\theta+\frac{\mathrm{4}}{\mathrm{5}}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$${let}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{4}}\right)=\mathrm{cos}\:\left(\mathrm{2}\theta−\alpha\right) \\ $$$$\Rightarrow\mathrm{2}\theta−\alpha=\mathrm{2}{k}\pi\pm\left(\theta−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\Rightarrow\mathrm{2}\theta−\alpha=\mathrm{2}{k}\pi+\theta−\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{4}}+\alpha\:{with}\:{k}=\mathrm{0} \\ $$$${or} \\ $$$$\Rightarrow\mathrm{2}\theta−\alpha=\mathrm{2}{k}\pi−\theta+\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{3}\theta=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{4}}+\alpha \\ $$$$\Rightarrow\theta_{\mathrm{2},\mathrm{3},\mathrm{4}} =\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{12}}+\frac{\alpha}{\mathrm{3}}\:{with}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$${since}\:\mathrm{cos}\:\theta\geqslant\mathrm{0},\:\mathrm{sin}\:\theta\geqslant\mathrm{0},\:{only}\:{valid}: \\ $$$$\theta_{\mathrm{1}} =−\frac{\pi}{\mathrm{4}}+\alpha \\ $$$$\theta_{\mathrm{2}} =\frac{\pi}{\mathrm{12}}+\frac{\alpha}{\mathrm{3}} \\ $$$${x}={p}^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:=\left(\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:=\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\left(−\frac{\pi}{\mathrm{4}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}}\right)−\mathrm{1}=\frac{\mathrm{24}}{\mathrm{25}}=\mathrm{0}.\mathrm{96} \\ $$$${or} \\ $$$$\:\:\:=\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}}\right)−\mathrm{1}\approx\mathrm{0}.\mathrm{415962} \\ $$
Answered by ajfour last updated on 23/Mar/21
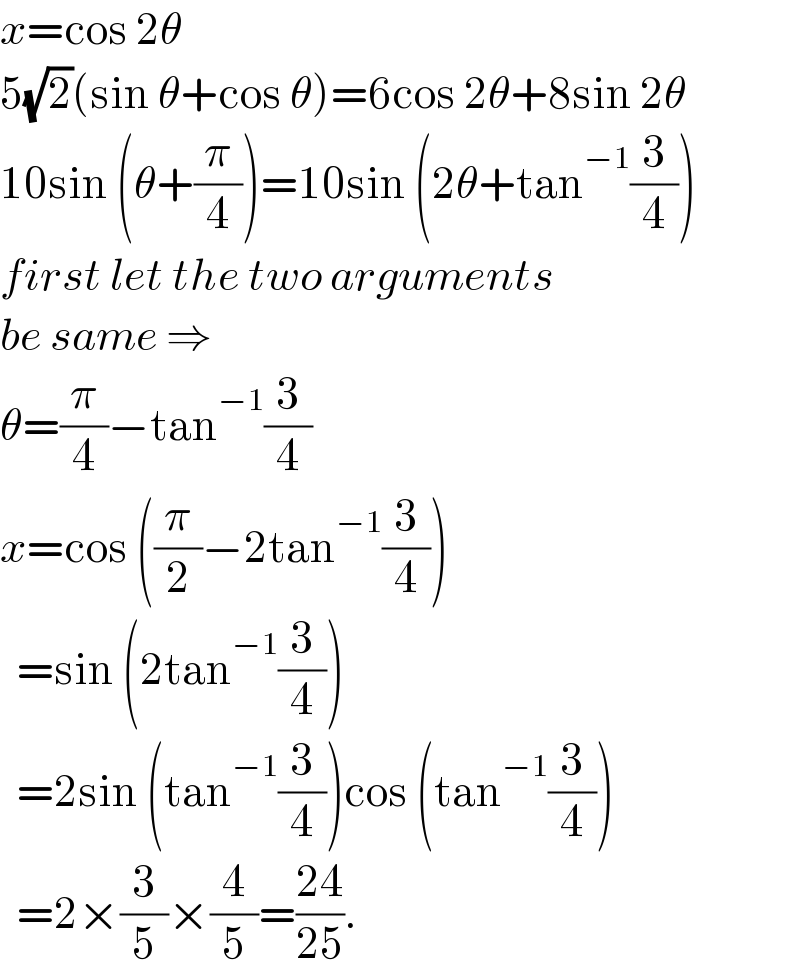
x=cos 2θ 5(√2)(sin θ+cos θ)=6cos 2θ+8sin 2θ 10sin (θ+(π/4))=10sin (2θ+tan^(−1) (3/4)) first let the two arguments be same ⇒ θ=(π/4)−tan^(−1) (3/4) x=cos ((π/2)−2tan^(−1) (3/4)) =sin (2tan^(−1) (3/4)) =2sin (tan^(−1) (3/4))cos (tan^(−1) (3/4)) =2×(3/5)×(4/5)=((24)/(25)).
$${x}=\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\mathrm{5}\sqrt{\mathrm{2}}\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)=\mathrm{6cos}\:\mathrm{2}\theta+\mathrm{8sin}\:\mathrm{2}\theta \\ $$$$\mathrm{10sin}\:\left(\theta+\frac{\pi}{\mathrm{4}}\right)=\mathrm{10sin}\:\left(\mathrm{2}\theta+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$${first}\:{let}\:{the}\:{two}\:{arguments} \\ $$$${be}\:{same}\:\Rightarrow \\ $$$$\theta=\frac{\pi}{\mathrm{4}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$$${x}=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\:\:=\mathrm{sin}\:\left(\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\:\:=\mathrm{2sin}\:\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\right)\mathrm{cos}\:\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\:\:=\mathrm{2}×\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{4}}{\mathrm{5}}=\frac{\mathrm{24}}{\mathrm{25}}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *