Menu Close

5-4-9-2-9-16-25-3-13-36-49-4-17-64-81-5-21-100-121-

Tinku Tara 0 Comments
Pin




Question Number 70783 by naka3546 last updated on 08/Oct/19
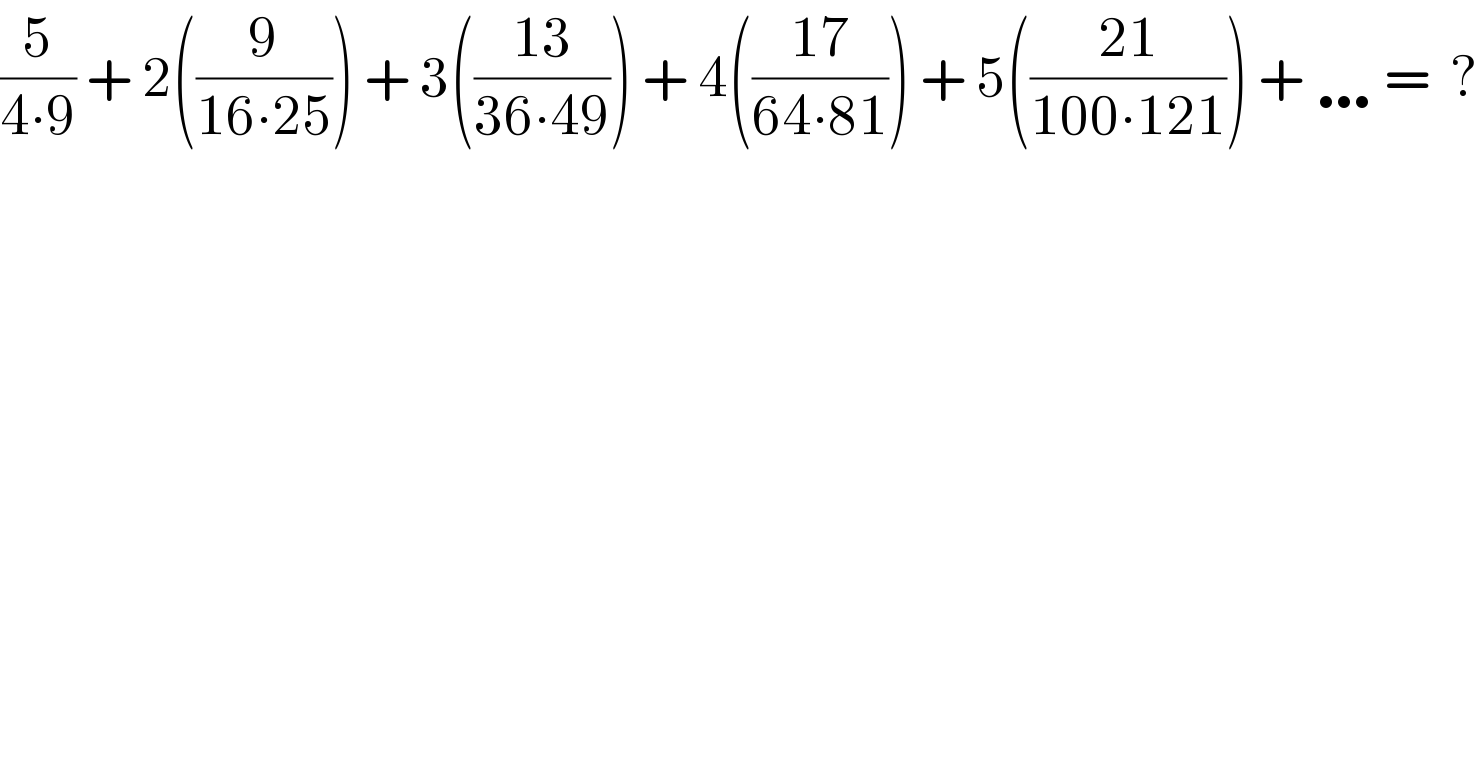
(5/(4∙9)) + 2((9/(16∙25))) + 3(((13)/(36∙49))) + 4(((17)/(64∙81))) + 5(((21)/(100∙121))) + … = ?
$$\frac{\mathrm{5}}{\mathrm{4}\centerdot\mathrm{9}}\:+\:\mathrm{2}\left(\frac{\mathrm{9}}{\mathrm{16}\centerdot\mathrm{25}}\right)\:+\:\mathrm{3}\left(\frac{\mathrm{13}}{\mathrm{36}\centerdot\mathrm{49}}\right)\:+\:\mathrm{4}\left(\frac{\mathrm{17}}{\mathrm{64}\centerdot\mathrm{81}}\right)\:+\:\mathrm{5}\left(\frac{\mathrm{21}}{\mathrm{100}\centerdot\mathrm{121}}\right)\:+\:\ldots\:=\:\:? \\ $$
Commented by tw000001 last updated on 08/Oct/19
Well,this one is unconverge series because difference and ratio are different. But the answer should be approximately on (1/5) with calculator.
$$\mathrm{Well},\mathrm{this}\:\mathrm{one}\:\mathrm{is}\:\mathrm{unconverge}\:\mathrm{series}\:\mathrm{because} \\ $$$$\mathrm{difference}\:\mathrm{and}\:\mathrm{ratio}\:\mathrm{are}\:\mathrm{different}. \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{should}\:\mathrm{be}\:\mathrm{approximately} \\ $$$$\mathrm{on}\:\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{with}\:\mathrm{calculator}. \\ $$
Commented by tw000001 last updated on 08/Oct/19
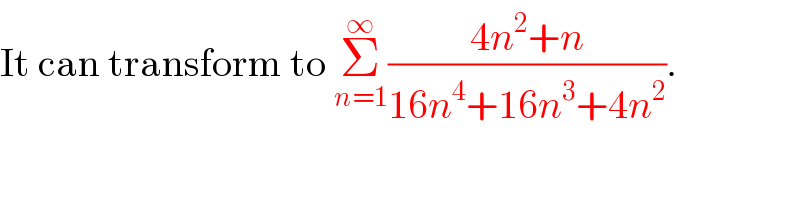
It can transform to Σ_(n=1) ^∞ ((4n^2 +n)/(16n^4 +16n^3 +4n^2 )).
$$\mathrm{It}\:\mathrm{can}\:\mathrm{transform}\:\mathrm{to}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}{n}^{\mathrm{2}} +{n}}{\mathrm{16}{n}^{\mathrm{4}} +\mathrm{16}{n}^{\mathrm{3}} +\mathrm{4}{n}^{\mathrm{2}} }. \\ $$
Commented by naka3546 last updated on 08/Oct/19
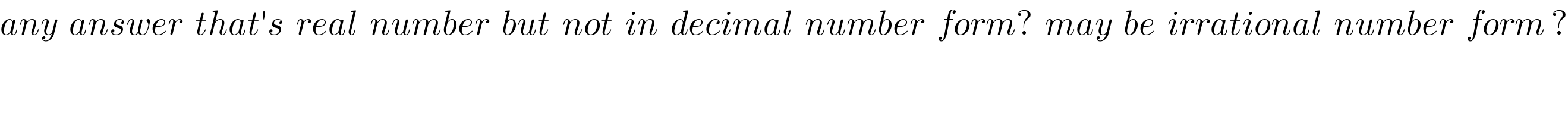
any answer that′s real number but not in decimal number form? may be irrational number form ?
$${any}\:\:{answer}\:\:{that}'{s}\:\:{real}\:\:{number}\:\:{but}\:\:{not}\:\:{in}\:\:{decimal}\:\:{number}\:\:{form}?\:\:{may}\:\:{be}\:\:{irrational}\:\:{number}\:\:{form}\:? \\ $$
Commented by prakash jain last updated on 08/Oct/19
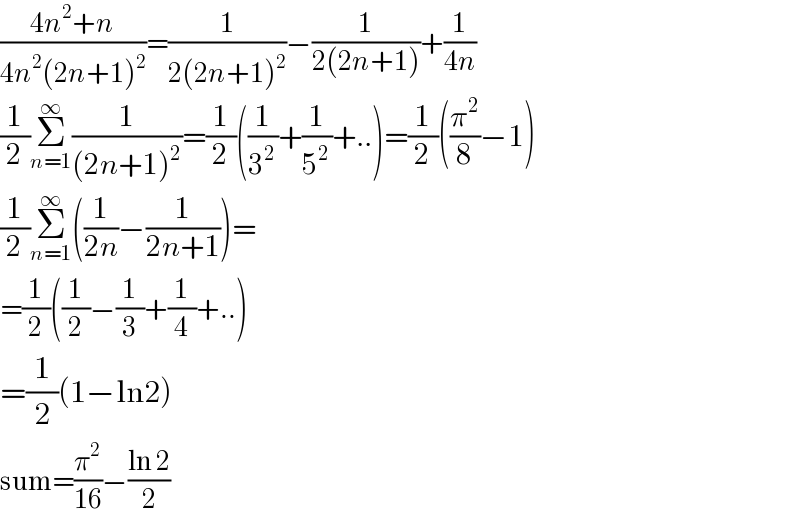
((4n^2 +n)/(4n^2 (2n+1)^2 ))=(1/(2(2n+1)^2 ))−(1/(2(2n+1)))+(1/(4n)) (1/2)Σ_(n=1) ^∞ (1/((2n+1)^2 ))=(1/2)((1/3^2 )+(1/5^2 )+..)=(1/2)((π^2 /8)−1) (1/2)Σ_(n=1) ^∞ ((1/(2n))−(1/(2n+1)))= =(1/2)((1/2)−(1/3)+(1/4)+..) =(1/2)(1−ln2) sum=(π^2 /(16))−((ln 2)/2)
$$\frac{\mathrm{4}{n}^{\mathrm{2}} +{n}}{\mathrm{4}{n}^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}{n}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+..\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+..\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{ln2}\right) \\ $$$$\mathrm{sum}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$
Answered by mind is power last updated on 08/Oct/19
=Σ_(n≥1) ((n(4n+1))/((2n)^2 (2n+1)^2 )) f(x)=((x(4x+1))/(4x^2 (2x+1)^2 ))=(b/((2x+1)^2 ))+(c/x)+(d/(2x+1)) b=(1/2), 2c+d=0 (1/(18))+c+(d/3)=(5/(36)) ⇒d+3c=(1/4) c=(1/4),d=((−1)/2) ((x(4x+1))/(4x^2 (2x+1)^2 ))=(1/(2(2x+1)^2 ))+(1/(4x))−(1/(2(2x+1))) Σ_(n≥1) f(n)=Σ(1/(2(2n+1)^2 ))+Σ(1/(4n))−(1/(4n+2)) =(1/2)Σ((1/((2n+1)^2 ))+(1/((2n)^2 ))−(1/((2n)^2 )))+(1/2)Σ(1/(2n))−(1/(2n+1)) =(1/2)Σ(1/n^2 )−(1/8)Σ(1/n^2 )+(1/2)Σ(1/(2n(2n+1))) =(3/8)ζ(2)+(1/2)Σ(x^(2n+1) /(2n(2n+1)))∣x=1 f(x)=(3/8)ζ(2)+(1/2)Σ(x^(2n+1) /(2n(2n+1))) f′(x)=(1/2)Σ(x^(2n) /(2n))=(1/4)Σ_(n≥1) (((x^2 )^n )/n)=−(1/4)ln(1−x^2 ) f(x)=−(1/4)∫ln(1−x^2 )dx =−(1/4)xln(1−x^2 )+(1/4)∫((−2x^2 )/(1−x^2 ))dx =−((xln(1−x^2 ))/4)−(1/2)∫−1+(1/(1−x^2 ))dx =((−xln(1−x^2 ))/4)+(x/2)−(1/2)∫(dx/((1−x)(1+x))) =((−xln(1−x^2 ))/4)+(x/2)−(1/4)∫(1/(1+x))dx−(1/4)∫(1/(1−x))dx =((−xln(1−x^2 ))/4)+(x/2)+(1/4)ln(((1−x)/(1+x)))+c f(0)=(3/8)ζ(2) ⇒ f(x)=((−xln(1−x)−xln(1+x)+2x+ln(1−x)−ln(1+x))/4)+((3ζ(2))/8) =(((1−x)ln(1−x)−(1+x)ln(1+x)+2x)/4)+((3ζ(2))/8) limx→1f(x)=((2−2ln(2))/4)+((3ζ(2))/8)=Σ_(n≥1) f(n) ⇒ Σ_(n≥1) ((n(4n+1))/((2n)^2 (2n+1)^2 ))=((2−2ln(2))/4)+(3/8).(π^2 /6)
$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{n}\left(\mathrm{4}{n}+\mathrm{1}\right)}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${f}\left({x}\right)=\frac{{x}\left(\mathrm{4}{x}+\mathrm{1}\right)}{\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{b}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{c}}{{x}}+\frac{{d}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{2}}, \\ $$$$\mathrm{2}{c}+{d}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{18}}+{c}+\frac{{d}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{36}} \\ $$$$\Rightarrow{d}+\mathrm{3}{c}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${c}=\frac{\mathrm{1}}{\mathrm{4}},{d}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{x}\left(\mathrm{4}{x}+\mathrm{1}\right)}{\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}{x}}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right)} \\ $$$$\sum_{{n}\geqslant\mathrm{1}} {f}\left({n}\right)=\Sigma\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\Sigma\frac{\mathrm{1}}{\mathrm{4}{n}}−\frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left(\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2n}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2n}\right)^{\mathrm{2}} }\right)+\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}}\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{\mathrm{1}}{\mathrm{2}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\zeta\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}\mid{x}=\mathrm{1} \\ $$$${f}\left({x}\right)=\frac{\mathrm{3}}{\mathrm{8}}\zeta\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}{n}}=\frac{\mathrm{1}}{\mathrm{4}}\sum_{{n}\geqslant\mathrm{1}} \frac{\left({x}^{\mathrm{2}} \right)^{{n}} }{{n}}=−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$${f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{4}}\int{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}{xln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{−\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{{xln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\int−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{−{xln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{4}}+\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)} \\ $$$$=\frac{−{xln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{4}}+\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{\mathrm{1}−{x}}{dx} \\ $$$$=\frac{−{xln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{4}}+\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)+{c} \\ $$$${f}\left(\mathrm{0}\right)=\frac{\mathrm{3}}{\mathrm{8}}\zeta\left(\mathrm{2}\right) \\ $$$$\Rightarrow \\ $$$${f}\left({x}\right)=\frac{−{xln}\left(\mathrm{1}−{x}\right)−{xln}\left(\mathrm{1}+{x}\right)+\mathrm{2}{x}+{ln}\left(\mathrm{1}−{x}\right)−{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{4}}+\frac{\mathrm{3}\zeta\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$=\frac{\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−{x}\right)−\left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}+{x}\right)+\mathrm{2}{x}}{\mathrm{4}}+\frac{\mathrm{3}\zeta\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$${limx}\rightarrow\mathrm{1}{f}\left({x}\right)=\frac{\mathrm{2}−\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{4}}+\frac{\mathrm{3}\zeta\left(\mathrm{2}\right)}{\mathrm{8}}=\sum_{{n}\geqslant\mathrm{1}} {f}\left({n}\right) \\ $$$$\Rightarrow \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{n}\left(\mathrm{4}{n}+\mathrm{1}\right)}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{2}−\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *