Question Number 4696 by love math last updated on 22/Feb/16
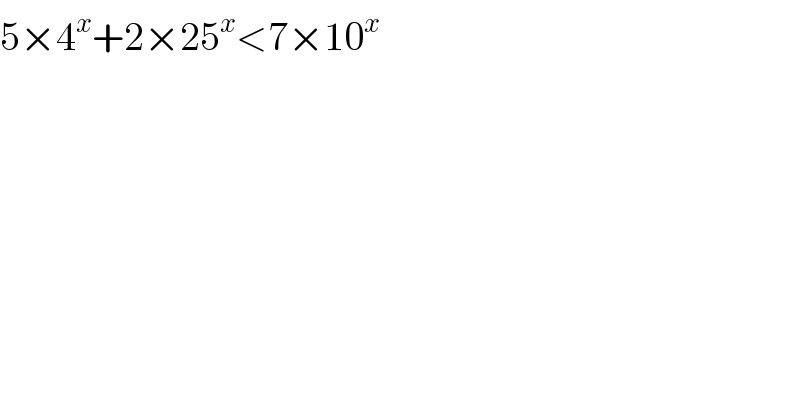
$$\mathrm{5}×\mathrm{4}^{{x}} +\mathrm{2}×\mathrm{25}^{{x}} <\mathrm{7}×\mathrm{10}^{{x}} \\ $$
Commented by prakash jain last updated on 22/Feb/16
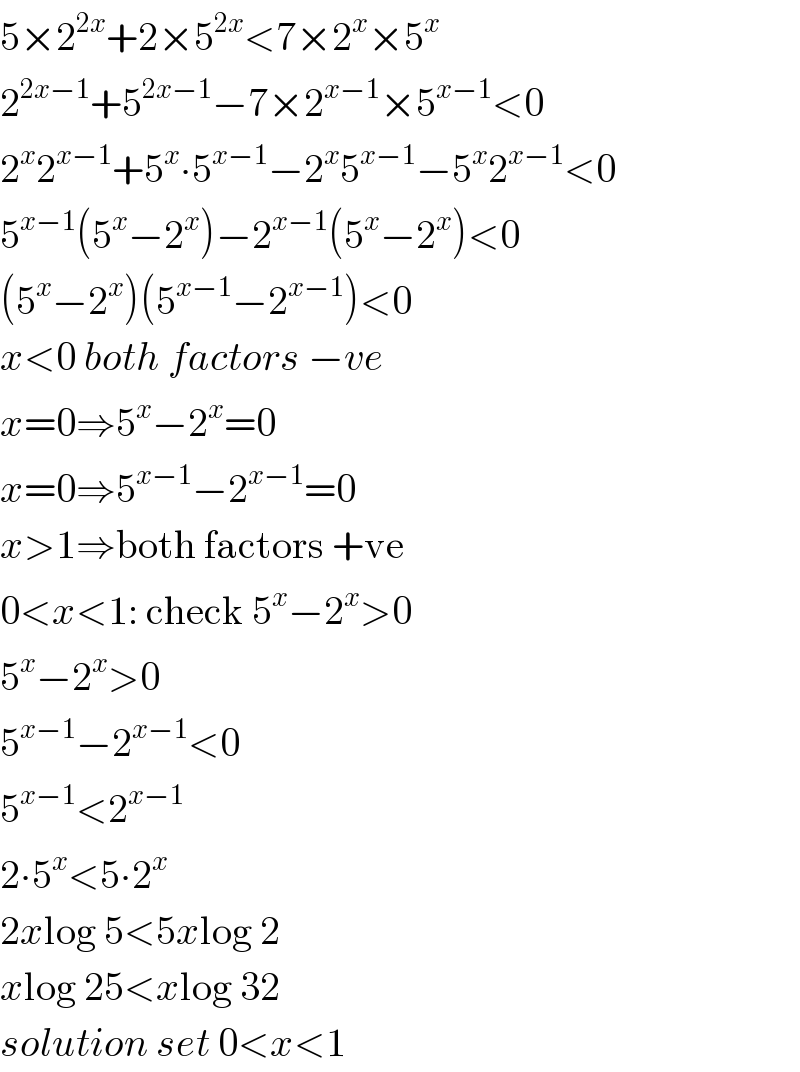
$$\mathrm{5}×\mathrm{2}^{\mathrm{2}{x}} +\mathrm{2}×\mathrm{5}^{\mathrm{2}{x}} <\mathrm{7}×\mathrm{2}^{{x}} ×\mathrm{5}^{{x}} \\ $$$$\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} +\mathrm{5}^{\mathrm{2}{x}−\mathrm{1}} −\mathrm{7}×\mathrm{2}^{{x}−\mathrm{1}} ×\mathrm{5}^{{x}−\mathrm{1}} <\mathrm{0} \\ $$$$\mathrm{2}^{{x}} \mathrm{2}^{{x}−\mathrm{1}} +\mathrm{5}^{{x}} \centerdot\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{2}^{{x}} \mathrm{5}^{{x}−\mathrm{1}} −\mathrm{5}^{{x}} \mathrm{2}^{{x}−\mathrm{1}} <\mathrm{0} \\ $$$$\mathrm{5}^{{x}−\mathrm{1}} \left(\mathrm{5}^{{x}} −\mathrm{2}^{{x}} \right)−\mathrm{2}^{{x}−\mathrm{1}} \left(\mathrm{5}^{{x}} −\mathrm{2}^{{x}} \right)<\mathrm{0} \\ $$$$\left(\mathrm{5}^{{x}} −\mathrm{2}^{{x}} \right)\left(\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{2}^{{x}−\mathrm{1}} \right)<\mathrm{0} \\ $$$${x}<\mathrm{0}\:{both}\:{factors}\:−{ve} \\ $$$${x}=\mathrm{0}\Rightarrow\mathrm{5}^{{x}} −\mathrm{2}^{{x}} =\mathrm{0} \\ $$$${x}=\mathrm{0}\Rightarrow\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{2}^{{x}−\mathrm{1}} =\mathrm{0} \\ $$$${x}>\mathrm{1}\Rightarrow\mathrm{both}\:\mathrm{factors}\:+\mathrm{ve} \\ $$$$\mathrm{0}<{x}<\mathrm{1}:\:\mathrm{check}\:\mathrm{5}^{{x}} −\mathrm{2}^{{x}} >\mathrm{0} \\ $$$$\mathrm{5}^{{x}} −\mathrm{2}^{{x}} >\mathrm{0} \\ $$$$\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{2}^{{x}−\mathrm{1}} <\mathrm{0} \\ $$$$\mathrm{5}^{{x}−\mathrm{1}} <\mathrm{2}^{{x}−\mathrm{1}} \\ $$$$\mathrm{2}\centerdot\mathrm{5}^{{x}} <\mathrm{5}\centerdot\mathrm{2}^{{x}} \\ $$$$\mathrm{2}{x}\mathrm{log}\:\mathrm{5}<\mathrm{5}{x}\mathrm{log}\:\mathrm{2} \\ $$$${x}\mathrm{log}\:\mathrm{25}<{x}\mathrm{log}\:\mathrm{32} \\ $$$${solution}\:{set}\:\mathrm{0}<{x}<\mathrm{1} \\ $$
