Question Number 6483 by sanusihammed last updated on 28/Jun/16
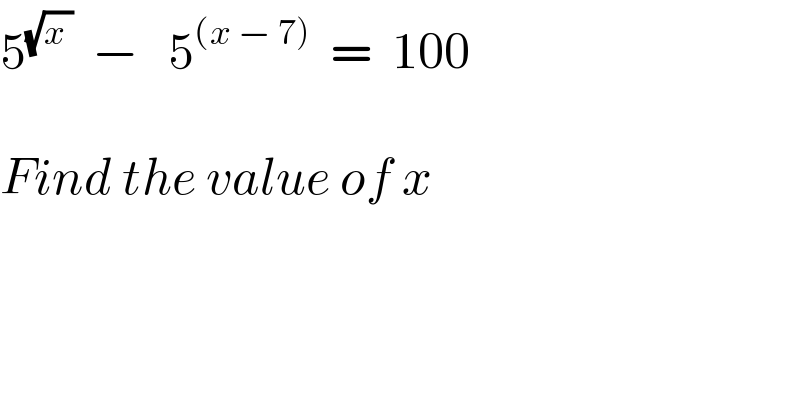
$$\mathrm{5}^{\sqrt{{x}\:}} \:\:−\:\:\:\mathrm{5}^{\left({x}\:−\:\mathrm{7}\right)} \:\:=\:\:\mathrm{100} \\ $$$$ \\ $$$${Find}\:{the}\:{value}\:{of}\:{x} \\ $$
Answered by Yozzii last updated on 29/Jun/16
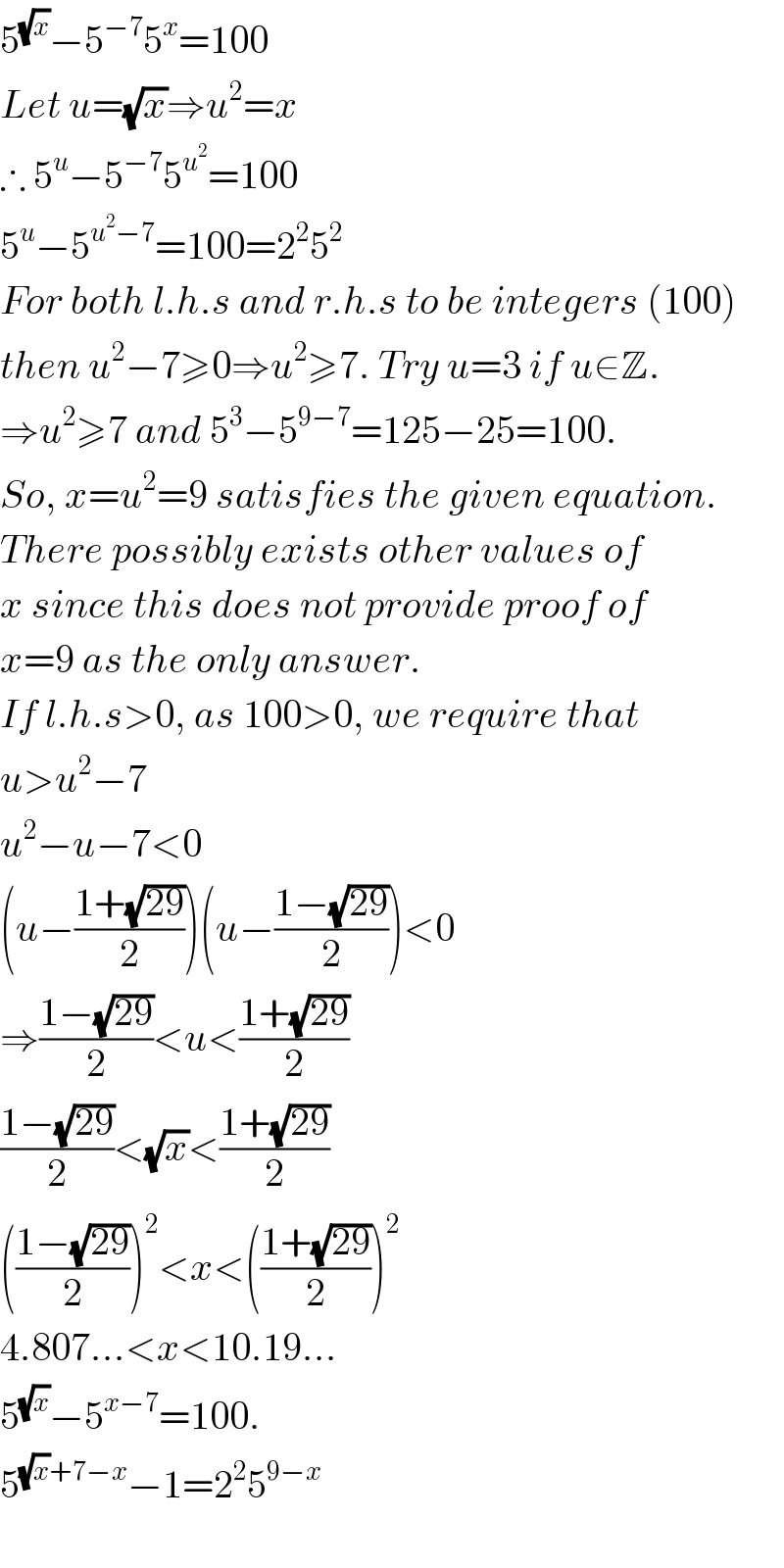
$$\mathrm{5}^{\sqrt{{x}}} −\mathrm{5}^{−\mathrm{7}} \mathrm{5}^{{x}} =\mathrm{100} \\ $$$${Let}\:{u}=\sqrt{{x}}\Rightarrow{u}^{\mathrm{2}} ={x} \\ $$$$\therefore\:\mathrm{5}^{{u}} −\mathrm{5}^{−\mathrm{7}} \mathrm{5}^{{u}^{\mathrm{2}} } =\mathrm{100} \\ $$$$\mathrm{5}^{{u}} −\mathrm{5}^{{u}^{\mathrm{2}} −\mathrm{7}} =\mathrm{100}=\mathrm{2}^{\mathrm{2}} \mathrm{5}^{\mathrm{2}} \\ $$$${For}\:{both}\:{l}.{h}.{s}\:{and}\:{r}.{h}.{s}\:{to}\:{be}\:{integers}\:\left(\mathrm{100}\right)\: \\ $$$${then}\:{u}^{\mathrm{2}} −\mathrm{7}\geqslant\mathrm{0}\Rightarrow{u}^{\mathrm{2}} \geqslant\mathrm{7}.\:{Try}\:{u}=\mathrm{3}\:{if}\:{u}\in\mathbb{Z}. \\ $$$$\Rightarrow{u}^{\mathrm{2}} \geqslant\mathrm{7}\:{and}\:\mathrm{5}^{\mathrm{3}} −\mathrm{5}^{\mathrm{9}−\mathrm{7}} =\mathrm{125}−\mathrm{25}=\mathrm{100}. \\ $$$${So},\:{x}={u}^{\mathrm{2}} =\mathrm{9}\:{satisfies}\:{the}\:{given}\:{equation}. \\ $$$${There}\:{possibly}\:{exists}\:{other}\:{values}\:{of} \\ $$$${x}\:{since}\:{this}\:{does}\:{not}\:{provide}\:{proof}\:{of} \\ $$$${x}=\mathrm{9}\:{as}\:{the}\:{only}\:{answer}. \\ $$$${If}\:{l}.{h}.{s}>\mathrm{0},\:{as}\:\mathrm{100}>\mathrm{0},\:{we}\:{require}\:{that} \\ $$$${u}>{u}^{\mathrm{2}} −\mathrm{7} \\ $$$${u}^{\mathrm{2}} −{u}−\mathrm{7}<\mathrm{0} \\ $$$$\left({u}−\frac{\mathrm{1}+\sqrt{\mathrm{29}}}{\mathrm{2}}\right)\left({u}−\frac{\mathrm{1}−\sqrt{\mathrm{29}}}{\mathrm{2}}\right)<\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}−\sqrt{\mathrm{29}}}{\mathrm{2}}<{u}<\frac{\mathrm{1}+\sqrt{\mathrm{29}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}−\sqrt{\mathrm{29}}}{\mathrm{2}}<\sqrt{{x}}<\frac{\mathrm{1}+\sqrt{\mathrm{29}}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}−\sqrt{\mathrm{29}}}{\mathrm{2}}\right)^{\mathrm{2}} <{x}<\left(\frac{\mathrm{1}+\sqrt{\mathrm{29}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}.\mathrm{807}…<{x}<\mathrm{10}.\mathrm{19}… \\ $$$$\mathrm{5}^{\sqrt{{x}}} −\mathrm{5}^{{x}−\mathrm{7}} =\mathrm{100}. \\ $$$$\mathrm{5}^{\sqrt{{x}}+\mathrm{7}−{x}} −\mathrm{1}=\mathrm{2}^{\mathrm{2}} \mathrm{5}^{\mathrm{9}−{x}} \\ $$$$ \\ $$
Commented by sanusihammed last updated on 29/Jun/16

$${Thanks}\:{so}\:{much} \\ $$
