500-108-54-and-15-are-are-not-perfect-cubes-how-do-we-factorize-1-500X-3-108Y-3-2-54X-3-15Y-3-please-help-me-with-well-explained-steps-or-shortcut-thanks-

Question Number 135656 by otchereabdullai@gmail.com last updated on 14/Mar/21

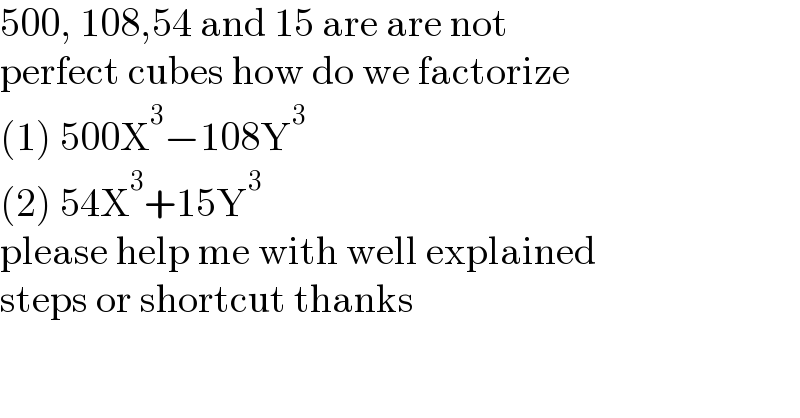
$$\mathrm{500},\:\mathrm{108},\mathrm{54}\:\mathrm{and}\:\mathrm{15}\:\mathrm{are}\:\mathrm{are}\:\mathrm{not}\: \\ $$$$\mathrm{perfect}\:\mathrm{cubes}\:\mathrm{how}\:\mathrm{do}\:\mathrm{we}\:\mathrm{factorize} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{500X}^{\mathrm{3}} −\mathrm{108Y}^{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{54X}^{\mathrm{3}} +\mathrm{15Y}^{\mathrm{3}} \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{with}\:\mathrm{well}\:\mathrm{explained}\: \\ $$$$\mathrm{steps}\:\mathrm{or}\:\mathrm{shortcut}\:\mathrm{thanks} \\ $$

Commented by MJS_new last updated on 14/Mar/21

$$\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{one}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{further}\:\mathrm{factorized} \\ $$

Answered by Olaf last updated on 14/Mar/21

$$\mathrm{500X}^{\mathrm{3}} −\mathrm{108Y}^{\mathrm{3}} \:=\:\mathrm{4}\left(\mathrm{125X}^{\mathrm{3}} −\mathrm{27Y}^{\mathrm{3}} \right) \\ $$$$=\:\mathrm{4}\left[\left(\mathrm{5X}\right)^{\mathrm{3}} −\left(\mathrm{3Y}\right)^{\mathrm{3}} \right] \\ $$$$=\:\mathrm{4}\left(\mathrm{5X}−\mathrm{3Y}\right)\left(\mathrm{25X}^{\mathrm{2}} +\mathrm{15XY}+\mathrm{9Y}^{\mathrm{2}} \right) \\ $$

Commented by otchereabdullai@gmail.com last updated on 14/Mar/21

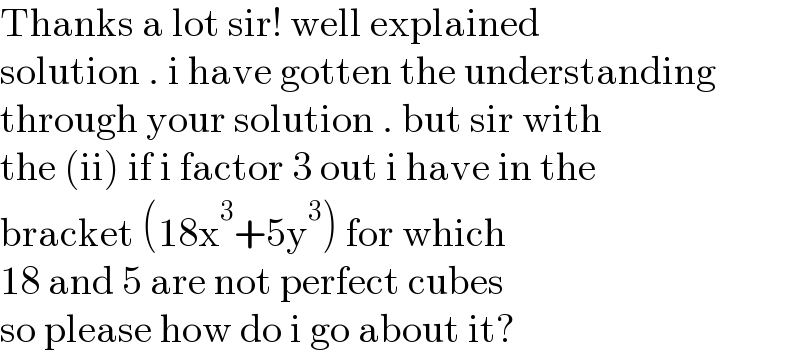
$$\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir}!\:\mathrm{well}\:\mathrm{explained}\: \\ $$$$\mathrm{solution}\:.\:\mathrm{i}\:\mathrm{have}\:\mathrm{gotten}\:\mathrm{the}\:\mathrm{understanding} \\ $$$$\mathrm{through}\:\mathrm{your}\:\mathrm{solution}\:.\:\mathrm{but}\:\mathrm{sir}\:\mathrm{with} \\ $$$$\mathrm{the}\:\left(\mathrm{ii}\right)\:\mathrm{if}\:\mathrm{i}\:\mathrm{factor}\:\mathrm{3}\:\mathrm{out}\:\mathrm{i}\:\mathrm{have}\:\mathrm{in}\:\mathrm{the}\: \\ $$$$\mathrm{bracket}\:\left(\mathrm{18x}^{\mathrm{3}} +\mathrm{5y}^{\mathrm{3}} \right)\:\mathrm{for}\:\mathrm{which} \\ $$$$\mathrm{18}\:\mathrm{and}\:\mathrm{5}\:\mathrm{are}\:\mathrm{not}\:\mathrm{perfect}\:\mathrm{cubes} \\ $$$$\mathrm{so}\:\mathrm{please}\:\mathrm{how}\:\mathrm{do}\:\mathrm{i}\:\mathrm{go}\:\mathrm{about}\:\mathrm{it}? \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com