5y-1-y-2-3-2-please-solve-the-differtial-equation-

Question Number 71516 by oyemi kemewari last updated on 16/Oct/19

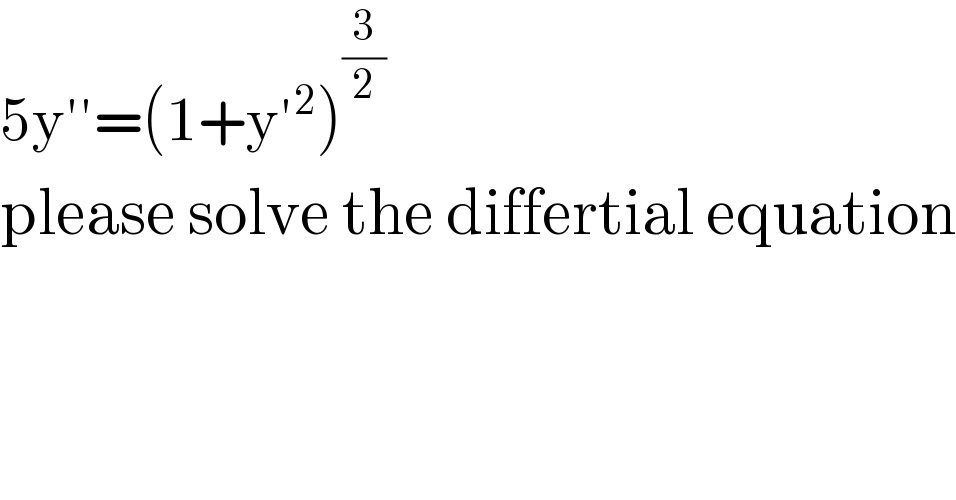
$$\mathrm{5y}''=\left(\mathrm{1}+\mathrm{y}'^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{please}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{differtial}\:\mathrm{equation} \\ $$

Answered by mind is power last updated on 17/Oct/19

let z=y′ 5z′=(1+z^2 )^(3/2) ⇒(dz/((1+z^2 )^(3/2) ))=dx z=tg(u) dz=(1+tg^2 (u))du ⇒(du/( (√(1+tg^2 (u)))))=(1/5)dx ⇒cos(u)=(x/5)+v u=arcos((x/5)+v) z=tg(u)=((√(1−((x/5)+v)^2 ))/((x/5)+v)) y=∫zdx=∫((√(1−((x/5)+v)))/((x/5)+v))dx =5∫((√(1−u))/u)du ,(√(1−u))=r⇒du=−2rdr 5∫((−2r^2 )/(1−r^2 ))dr=−10∫−1+(1/(1−r^2 ))dr=10r−10∫((1/(2(1−r)))+(1/(2(1+r))))dr =10r−5ln∣1−r^2 ∣ y=10(√(1−((x/5)+v)))−5ln∣(x/5)+v∣+c

$$\mathrm{let}\:\mathrm{z}=\mathrm{y}' \\ $$$$\mathrm{5z}'=\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\Rightarrow\frac{\mathrm{dz}}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\mathrm{dx} \\ $$$$\mathrm{z}=\mathrm{tg}\left(\mathrm{u}\right) \\ $$$$\mathrm{dz}=\left(\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\mathrm{u}\right)\right)\mathrm{du} \\ $$$$\Rightarrow\frac{\mathrm{du}}{\:\sqrt{\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\mathrm{u}\right)}}=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{dx} \\ $$$$\Rightarrow\mathrm{cos}\left(\mathrm{u}\right)=\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v} \\ $$$$\mathrm{u}=\mathrm{arcos}\left(\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v}\right) \\ $$$$\mathrm{z}=\mathrm{tg}\left(\mathrm{u}\right)=\frac{\sqrt{\mathrm{1}−\left(\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v}\right)^{\mathrm{2}} }}{\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v}} \\ $$$$\mathrm{y}=\int\mathrm{zdx}=\int\frac{\sqrt{\mathrm{1}−\left(\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v}\right)}}{\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v}}\mathrm{dx} \\ $$$$=\mathrm{5}\int\frac{\sqrt{\mathrm{1}−\mathrm{u}}}{\mathrm{u}}\mathrm{du}\:,\sqrt{\mathrm{1}−\mathrm{u}}=\mathrm{r}\Rightarrow\mathrm{du}=−\mathrm{2rdr} \\ $$$$\mathrm{5}\int\frac{−\mathrm{2r}^{\mathrm{2}} }{\mathrm{1}−\mathrm{r}^{\mathrm{2}} }\mathrm{dr}=−\mathrm{10}\int−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{r}^{\mathrm{2}} }\mathrm{dr}=\mathrm{10r}−\mathrm{10}\int\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{r}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{r}\right)}\right)\mathrm{dr} \\ $$$$=\mathrm{10r}−\mathrm{5ln}\mid\mathrm{1}−\mathrm{r}^{\mathrm{2}} \mid \\ $$$$\mathrm{y}=\mathrm{10}\sqrt{\mathrm{1}−\left(\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v}\right)}−\mathrm{5ln}\mid\frac{\mathrm{x}}{\mathrm{5}}+\mathrm{v}\mid+\mathrm{c} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

5y-1-y-2-3-2-please-solve-the-differtial-equation-

Leave a Reply Cancel reply