Question Number 8527 by suci last updated on 14/Oct/16
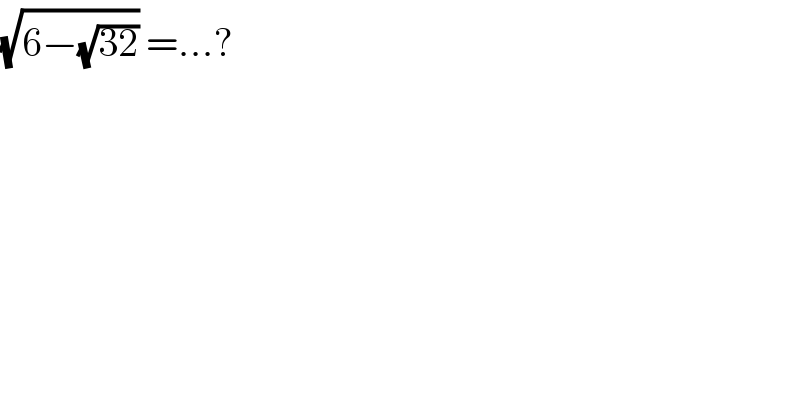
$$\sqrt{\mathrm{6}−\sqrt{\mathrm{32}}}\:=…? \\ $$
Answered by prakash jain last updated on 14/Oct/16
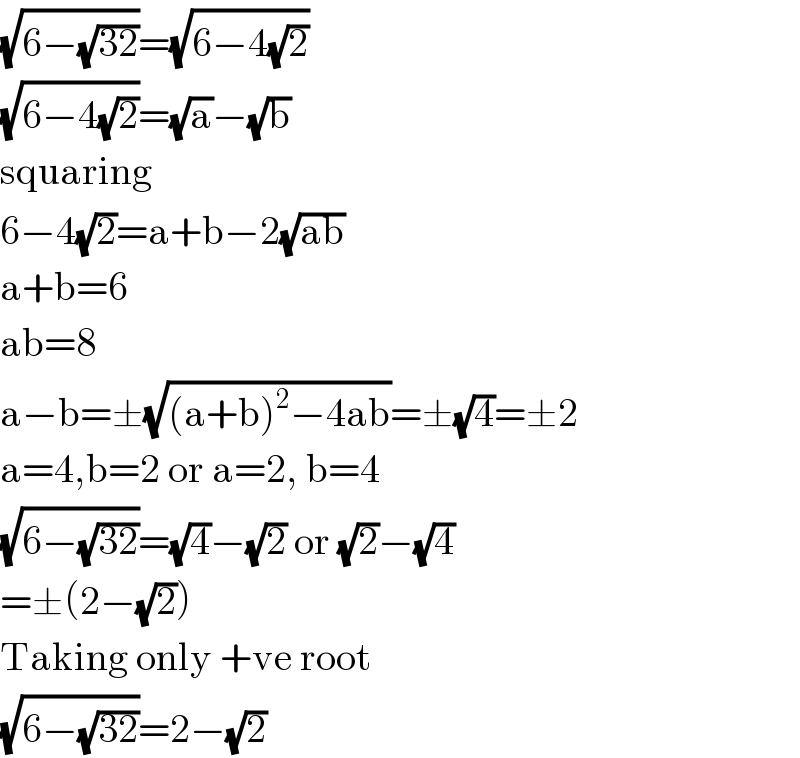
$$\sqrt{\mathrm{6}−\sqrt{\mathrm{32}}}=\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}=\sqrt{\mathrm{a}}−\sqrt{\mathrm{b}} \\ $$$$\mathrm{squaring} \\ $$$$\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}=\mathrm{a}+\mathrm{b}−\mathrm{2}\sqrt{\mathrm{ab}} \\ $$$$\mathrm{a}+\mathrm{b}=\mathrm{6} \\ $$$$\mathrm{ab}=\mathrm{8} \\ $$$$\mathrm{a}−\mathrm{b}=\pm\sqrt{\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} −\mathrm{4ab}}=\pm\sqrt{\mathrm{4}}=\pm\mathrm{2} \\ $$$$\mathrm{a}=\mathrm{4},\mathrm{b}=\mathrm{2}\:\mathrm{or}\:\mathrm{a}=\mathrm{2},\:\mathrm{b}=\mathrm{4} \\ $$$$\sqrt{\mathrm{6}−\sqrt{\mathrm{32}}}=\sqrt{\mathrm{4}}−\sqrt{\mathrm{2}}\:\mathrm{or}\:\sqrt{\mathrm{2}}−\sqrt{\mathrm{4}} \\ $$$$=\pm\left(\mathrm{2}−\sqrt{\mathrm{2}}\right) \\ $$$$\mathrm{Taking}\:\mathrm{only}\:+\mathrm{ve}\:\mathrm{root} \\ $$$$\sqrt{\mathrm{6}−\sqrt{\mathrm{32}}}=\mathrm{2}−\sqrt{\mathrm{2}} \\ $$
