Question Number 8281 by tawakalitu last updated on 06/Oct/16
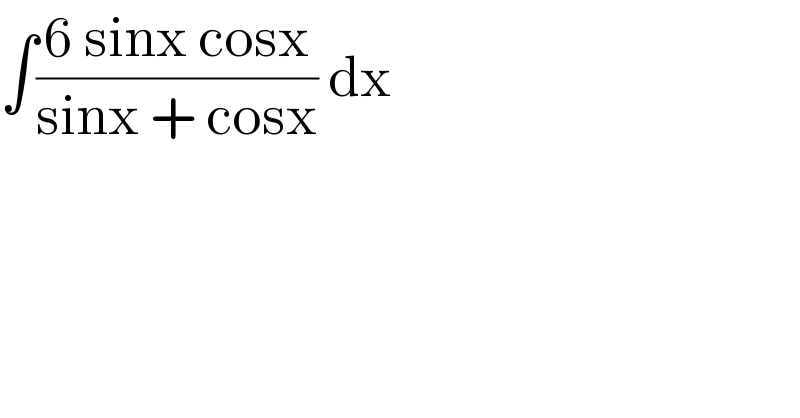
$$\int\frac{\mathrm{6}\:\mathrm{sinx}\:\mathrm{cosx}}{\mathrm{sinx}\:+\:\mathrm{cosx}}\:\mathrm{dx} \\ $$
Answered by Yozzias last updated on 06/Oct/16
![((sinx)/(sinx+cosx))=1−((cosx)/(sinx+cosx)) ∴ I=∫((sinxcosx)/(sinx+cosx))dx=∫(1−((cosx)/(sinx+cosx)))cosxdx =∫(cosx−((cos^2 x)/(sinx+cosx)))dx =∫(cosx−(1/2)(1+cos2x)((cosx−sinx)/(cos^2 x−sin^2 x)))dx =∫(cosx−((cosx−sinx)/(2cos2x))−((cos2x(cosx−sinx))/(2cos2x)))dx =∫(cosx−(1/(2(cosx+sinx)))+(1/2)sinx−(1/2)cosx)dx I=(1/2)∫(sinx+cosx−(1/(cosx+sinx)))dx ∵ cosx+sinx=(√2)cos(x−(π/4)) I=(1/2)∫(sinx+cosx−(1/( (√2)cos(x−(π/4)))))dx I=(1/2)∫(sinx+cosx−(1/( (√2)))sec(x−(π/4)))dx I=(1/2)[−cosx+sinx−(1/( (√2)))ln∣sec(x−(π/4))+tan(x−(π/4))∣]+c ∴ ∫((6sinxcosx)/(sinx+cosx))dx=3(sinx−cosx−((√2)/2)ln∣sec(x−(π/4))+tan(x−(π/4))∣)+c](https://www.tinkutara.com/question/Q8286.png)
$$\frac{\mathrm{sinx}}{\mathrm{sinx}+\mathrm{cosx}}=\mathrm{1}−\frac{\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}} \\ $$$$\therefore\:\mathrm{I}=\int\frac{\mathrm{sinxcosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}=\int\left(\mathrm{1}−\frac{\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}}\right)\mathrm{cosxdx} \\ $$$$=\int\left(\mathrm{cosx}−\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinx}+\mathrm{cosx}}\right)\mathrm{dx} \\ $$$$=\int\left(\mathrm{cosx}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos2x}\right)\frac{\mathrm{cosx}−\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx} \\ $$$$=\int\left(\mathrm{cosx}−\frac{\mathrm{cosx}−\mathrm{sinx}}{\mathrm{2cos2x}}−\frac{\mathrm{cos2x}\left(\mathrm{cosx}−\mathrm{sinx}\right)}{\mathrm{2cos2x}}\right)\mathrm{dx} \\ $$$$=\int\left(\mathrm{cosx}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{cosx}+\mathrm{sinx}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosx}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{sinx}+\mathrm{cosx}−\frac{\mathrm{1}}{\mathrm{cosx}+\mathrm{sinx}}\right)\mathrm{dx} \\ $$$$\because\:\mathrm{cosx}+\mathrm{sinx}=\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{sinx}+\mathrm{cosx}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{sinx}+\mathrm{cosx}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sec}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\right)\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\left[−\mathrm{cosx}+\mathrm{sinx}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\mid\mathrm{sec}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\mid\right]+\mathrm{c} \\ $$$$\therefore\:\int\frac{\mathrm{6sinxcosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}=\mathrm{3}\left(\mathrm{sinx}−\mathrm{cosx}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{sec}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\mid\right)+\mathrm{c} \\ $$$$ \\ $$
Commented by tawakalitu last updated on 06/Oct/16
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}\: \\ $$
