Question Number 11935 by uni last updated on 05/Apr/17
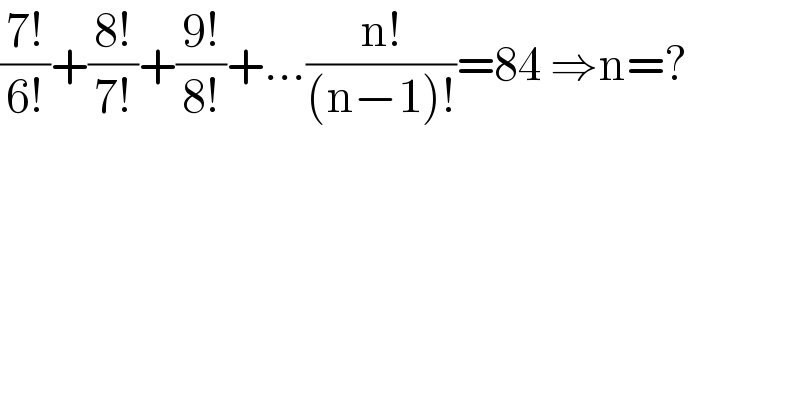
$$\frac{\mathrm{7}!}{\mathrm{6}!}+\frac{\mathrm{8}!}{\mathrm{7}!}+\frac{\mathrm{9}!}{\mathrm{8}!}+…\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{1}\right)!}=\mathrm{84}\:\Rightarrow\mathrm{n}=? \\ $$
Answered by bahmanfeshki1 last updated on 06/Apr/17

$${n}=\mathrm{14} \\ $$
Answered by ajfour last updated on 06/Apr/17
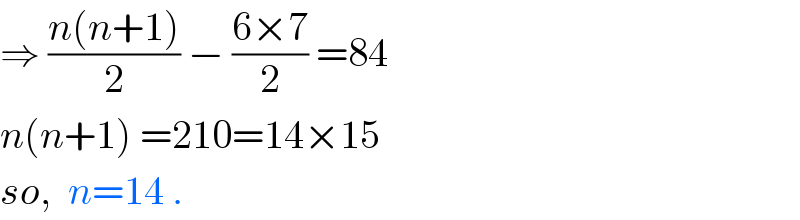
$$\Rightarrow\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:−\:\frac{\mathrm{6}×\mathrm{7}}{\mathrm{2}}\:=\mathrm{84} \\ $$$${n}\left({n}+\mathrm{1}\right)\:=\mathrm{210}=\mathrm{14}×\mathrm{15} \\ $$$${so},\:\:{n}=\mathrm{14}\:. \\ $$
Answered by sma3l2996 last updated on 06/Apr/17
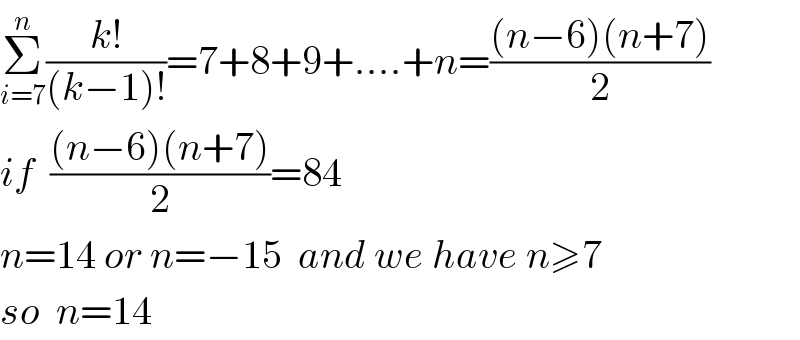
$$\underset{{i}=\mathrm{7}} {\overset{{n}} {\sum}}\frac{{k}!}{\left({k}−\mathrm{1}\right)!}=\mathrm{7}+\mathrm{8}+\mathrm{9}+….+{n}=\frac{\left({n}−\mathrm{6}\right)\left({n}+\mathrm{7}\right)}{\mathrm{2}} \\ $$$${if}\:\:\frac{\left({n}−\mathrm{6}\right)\left({n}+\mathrm{7}\right)}{\mathrm{2}}=\mathrm{84} \\ $$$${n}=\mathrm{14}\:{or}\:{n}=−\mathrm{15}\:\:{and}\:{we}\:{have}\:{n}\geqslant\mathrm{7} \\ $$$${so}\:\:{n}=\mathrm{14} \\ $$
