Question Number 11901 by ahmet last updated on 04/Apr/17
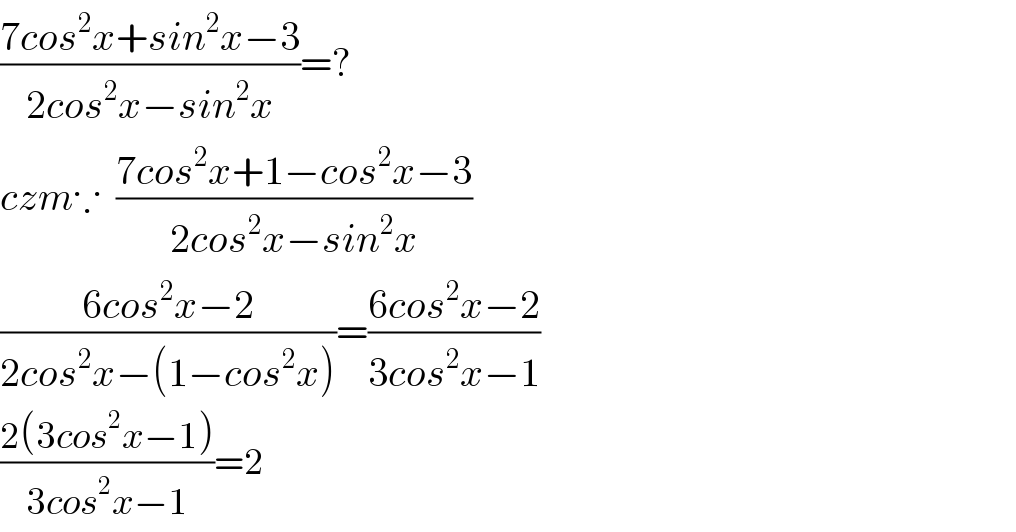
$$\frac{\mathrm{7}{cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}−\mathrm{3}}{\mathrm{2}{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}}=? \\ $$$${czm}\because\:\:\frac{\mathrm{7}{cos}^{\mathrm{2}} {x}+\mathrm{1}−{cos}^{\mathrm{2}} {x}−\mathrm{3}}{\mathrm{2}{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}} \\ $$$$\frac{\mathrm{6}{cos}^{\mathrm{2}} {x}−\mathrm{2}}{\mathrm{2}{cos}^{\mathrm{2}} {x}−\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)}=\frac{\mathrm{6}{cos}^{\mathrm{2}} {x}−\mathrm{2}}{\mathrm{3}{cos}^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$\frac{\mathrm{2}\left(\mathrm{3}{cos}^{\mathrm{2}} {x}−\mathrm{1}\right)}{\mathrm{3}{cos}^{\mathrm{2}} {x}−\mathrm{1}}=\mathrm{2} \\ $$
