Question Number 138980 by 7770 last updated on 20/Apr/21
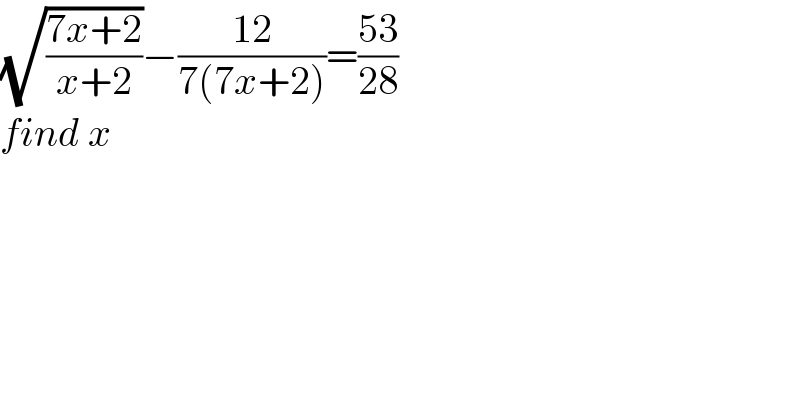
$$\sqrt{\frac{\mathrm{7}{x}+\mathrm{2}}{{x}+\mathrm{2}}}−\frac{\mathrm{12}}{\mathrm{7}\left(\mathrm{7}{x}+\mathrm{2}\right)}=\frac{\mathrm{53}}{\mathrm{28}} \\ $$$${find}\:{x} \\ $$
Answered by MJS_new last updated on 21/Apr/21
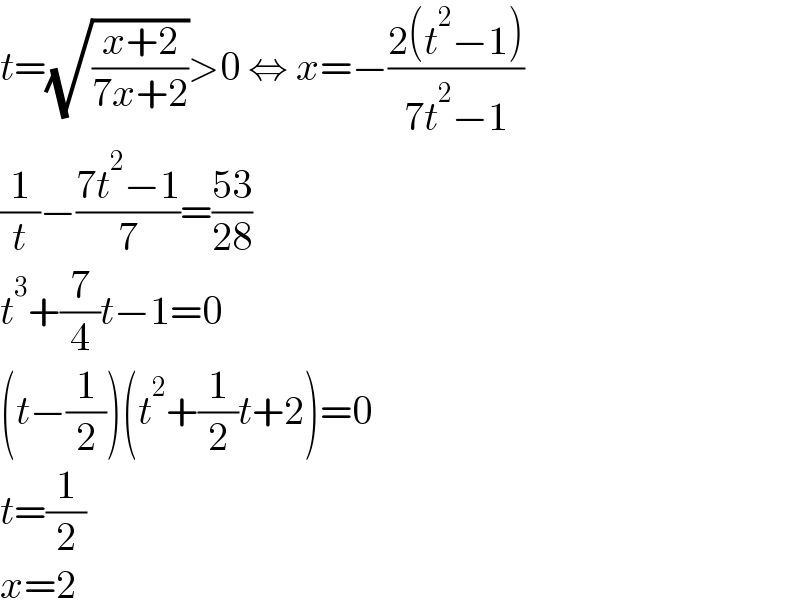
$${t}=\sqrt{\frac{{x}+\mathrm{2}}{\mathrm{7}{x}+\mathrm{2}}}>\mathrm{0}\:\Leftrightarrow\:{x}=−\frac{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{7}{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{t}}−\frac{\mathrm{7}{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{53}}{\mathrm{28}} \\ $$$${t}^{\mathrm{3}} +\frac{\mathrm{7}}{\mathrm{4}}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{t}+\mathrm{2}\right)=\mathrm{0} \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}=\mathrm{2} \\ $$
