Menu Close

8-log-6-x-17-log-x-6-7-

Tinku Tara 0 Comments
Pin




Question Number 66413 by hmamarques1994@gmail.com last updated on 14/Aug/19
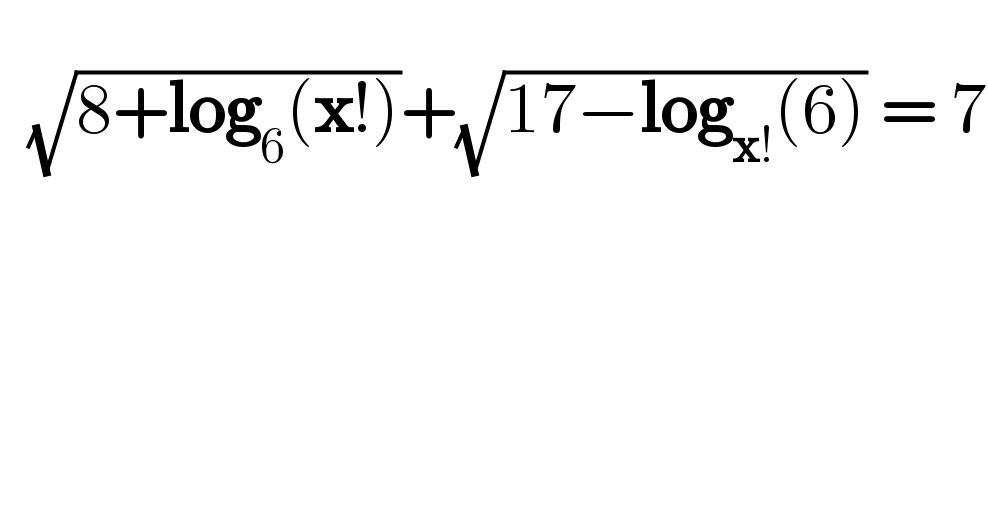
(√(8+log_6 (x!)))+(√(17−log_(x!) (6))) = 7
$$\: \\ $$$$\:\:\sqrt{\mathrm{8}+\boldsymbol{\mathrm{log}}_{\mathrm{6}} \left(\boldsymbol{\mathrm{x}}!\right)}+\sqrt{\mathrm{17}−\boldsymbol{\mathrm{log}}_{\boldsymbol{\mathrm{x}}!} \left(\mathrm{6}\right)}\:=\:\mathrm{7} \\ $$$$\: \\ $$
Answered by MJS last updated on 14/Aug/19
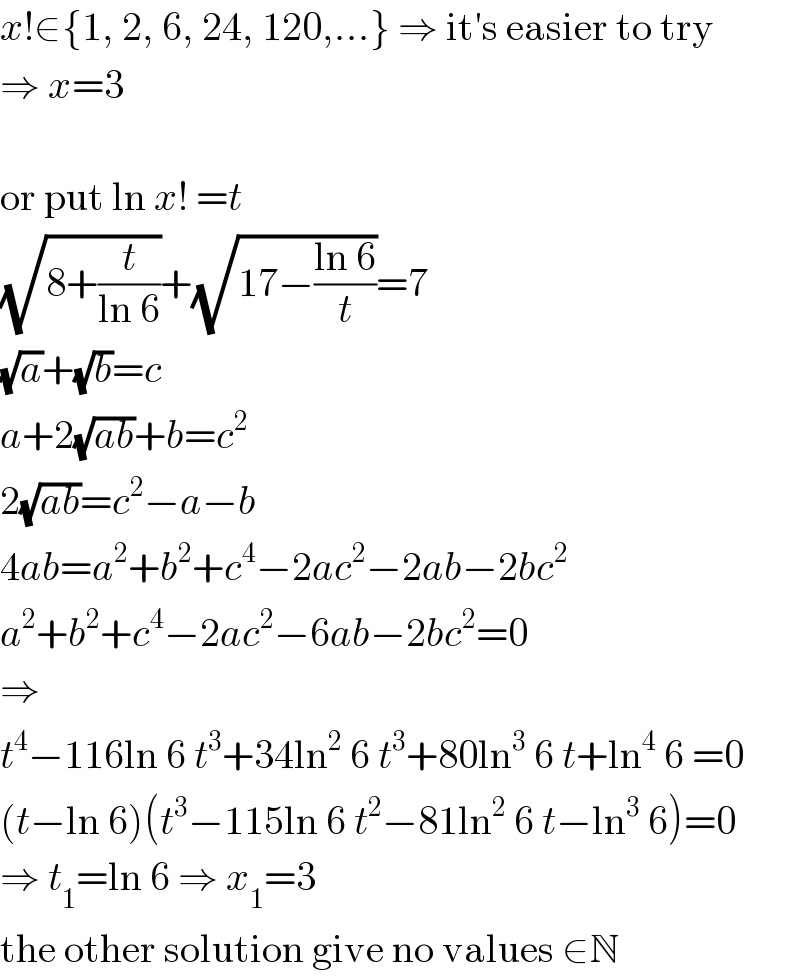
x!∈{1, 2, 6, 24, 120,...} ⇒ it′s easier to try ⇒ x=3 or put ln x! =t (√(8+(t/(ln 6))))+(√(17−((ln 6)/t)))=7 (√a)+(√b)=c a+2(√(ab))+b=c^2 2(√(ab))=c^2 −a−b 4ab=a^2 +b^2 +c^4 −2ac^2 −2ab−2bc^2 a^2 +b^2 +c^4 −2ac^2 −6ab−2bc^2 =0 ⇒ t^4 −116ln 6 t^3 +34ln^2 6 t^3 +80ln^3 6 t+ln^4 6 =0 (t−ln 6)(t^3 −115ln 6 t^2 −81ln^2 6 t−ln^3 6)=0 ⇒ t_1 =ln 6 ⇒ x_1 =3 the other solution give no values ∈N
$${x}!\in\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{6},\:\mathrm{24},\:\mathrm{120},…\right\}\:\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{easier}\:\mathrm{to}\:\mathrm{try} \\ $$$$\Rightarrow\:{x}=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{or}\:\mathrm{put}\:\mathrm{ln}\:{x}!\:={t} \\ $$$$\sqrt{\mathrm{8}+\frac{{t}}{\mathrm{ln}\:\mathrm{6}}}+\sqrt{\mathrm{17}−\frac{\mathrm{ln}\:\mathrm{6}}{{t}}}=\mathrm{7} \\ $$$$\sqrt{{a}}+\sqrt{{b}}={c} \\ $$$${a}+\mathrm{2}\sqrt{{ab}}+{b}={c}^{\mathrm{2}} \\ $$$$\mathrm{2}\sqrt{{ab}}={c}^{\mathrm{2}} −{a}−{b} \\ $$$$\mathrm{4}{ab}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{4}} −\mathrm{2}{ac}^{\mathrm{2}} −\mathrm{2}{ab}−\mathrm{2}{bc}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{4}} −\mathrm{2}{ac}^{\mathrm{2}} −\mathrm{6}{ab}−\mathrm{2}{bc}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{4}} −\mathrm{116ln}\:\mathrm{6}\:{t}^{\mathrm{3}} +\mathrm{34ln}^{\mathrm{2}} \:\mathrm{6}\:{t}^{\mathrm{3}} +\mathrm{80ln}^{\mathrm{3}} \:\mathrm{6}\:{t}+\mathrm{ln}^{\mathrm{4}} \:\mathrm{6}\:=\mathrm{0} \\ $$$$\left({t}−\mathrm{ln}\:\mathrm{6}\right)\left({t}^{\mathrm{3}} −\mathrm{115ln}\:\mathrm{6}\:{t}^{\mathrm{2}} −\mathrm{81ln}^{\mathrm{2}} \:\mathrm{6}\:{t}−\mathrm{ln}^{\mathrm{3}} \:\mathrm{6}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}_{\mathrm{1}} =\mathrm{ln}\:\mathrm{6}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{3} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{solution}\:\mathrm{give}\:\mathrm{no}\:\mathrm{values}\:\in\mathbb{N} \\ $$
Commented by hmamarques1994@gmai.com last updated on 14/Aug/19
Good!
$$\: \\ $$$$\:{Good}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *