8x-3-6x-1-0-Solves-

Question Number 11672 by @ANTARES_VY last updated on 29/Mar/17

8 x^{3} - 6 x + 1 = 0

Solves \dots

Commented by mrW1 last updated on 29/Mar/17

s e e g e n e r a l s o l u t i o n :

Commented by mrW1 last updated on 29/Mar/17

Commented by @ANTARES_VY last updated on 30/Mar/17

which program told

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17

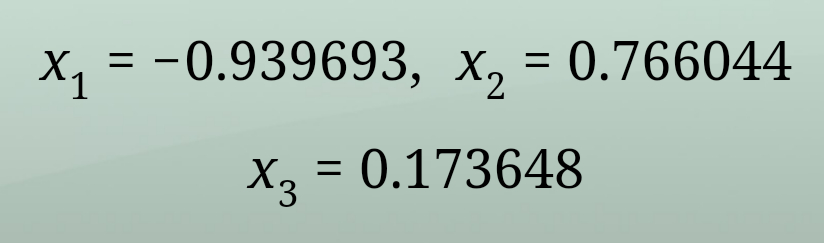
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17

Δ = b^{2} - 3 a c = 0 - 3 \times 8 \times (- 6) = 144 ⟩ 0

k = \frac{- 27 a^{2} d}{2 \sqrt{Δ^{3}}} = - 0.5 \Rightarrow∣ k ∣⩽ 1

x_{1} = \frac{2 \sqrt{Δ .} c o s (\frac{1}{3} {c o s}^{- 1} k) - b}{3 a} \frac{}{} =

x_{1} = \frac{- 2 \times 12 c o s (20) - 0}{3 \times 8} = \frac{24 \times 0.9396}{24} = - 0.9396

x_{2} = \frac{- 2 \times 12 c o s (20 - 120)}{24} = 0.1736

x_{3} = \frac{- 2 \times 12 c o s (20 + 120)}{24} = 0.7660

Commented by @ANTARES_VY last updated on 30/Mar/17

8 x^{3} - 6 x + 1 = 0 this development

is an example ?