Question Number 136906 by leena12345 last updated on 27/Mar/21
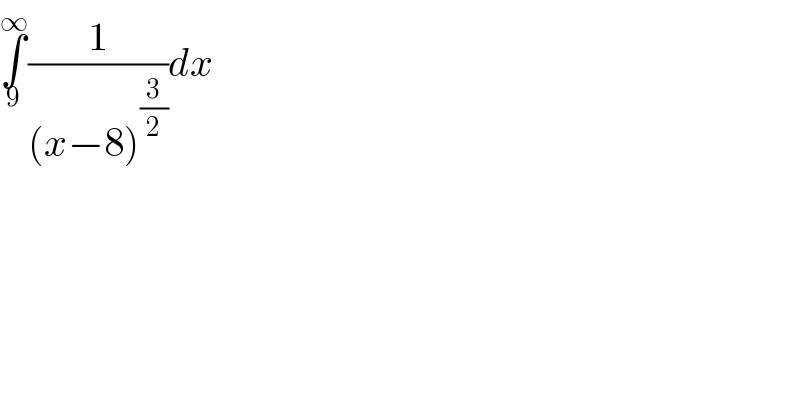
$$\underset{\mathrm{9}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{\left({x}−\mathrm{8}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 27/Mar/21
![=−2[(x−8)^(−(1/2)) ]_9 ^∞ =−2(−1)=2](https://www.tinkutara.com/question/Q136911.png)
$$=−\mathrm{2}\left[\left({x}−\mathrm{8}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right]_{\mathrm{9}} ^{\infty} =−\mathrm{2}\left(−\mathrm{1}\right)=\mathrm{2} \\ $$
Answered by Mathspace last updated on 27/Mar/21
![I =∫_9 ^∞ (dx/((x−8)^(3/2) ))=_(x−8=t) ∫_1 ^∞ (dt/t^(3/2) ) =∫_1 ^∞ t^(−(3/2)) dt =[(1/(−(3/2)+1))t^(−(3/2)+1) ]_1 ^∞ =[−2 t^(−(1/2)) ]_1 ^∞ =−2[(1/( (√t)))]_1 ^∞ =−2(−1) =2](https://www.tinkutara.com/question/Q136914.png)
$${I}\:=\int_{\mathrm{9}} ^{\infty} \:\frac{{dx}}{\left({x}−\mathrm{8}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=_{{x}−\mathrm{8}={t}} \:\int_{\mathrm{1}} ^{\infty} \:\frac{{dt}}{{t}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\int_{\mathrm{1}} ^{\infty} \:{t}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{dt}\:=\left[\frac{\mathrm{1}}{−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}}{t}^{−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}} \right]_{\mathrm{1}} ^{\infty} \\ $$$$=\left[−\mathrm{2}\:{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right]_{\mathrm{1}} ^{\infty} \:=−\mathrm{2}\left[\frac{\mathrm{1}}{\:\sqrt{{t}}}\right]_{\mathrm{1}} ^{\infty} \\ $$$$=−\mathrm{2}\left(−\mathrm{1}\right)\:=\mathrm{2} \\ $$
