Question Number 10289 by konen last updated on 02/Feb/17
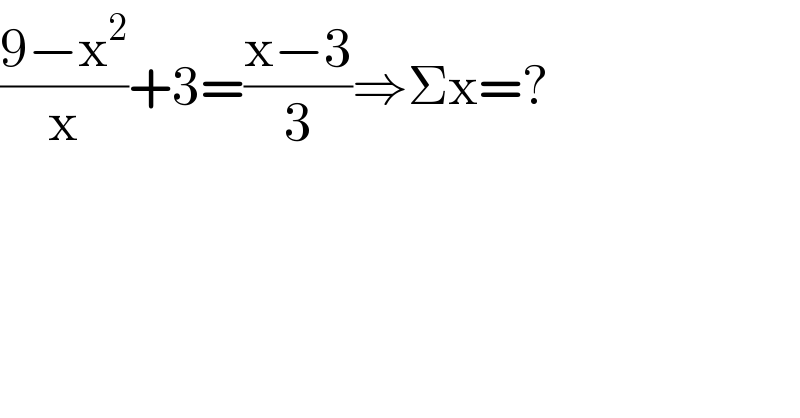
$$\frac{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}+\mathrm{3}=\frac{\mathrm{x}−\mathrm{3}}{\mathrm{3}}\Rightarrow\Sigma\mathrm{x}=? \\ $$$$ \\ $$
Answered by ridwan balatif last updated on 02/Feb/17
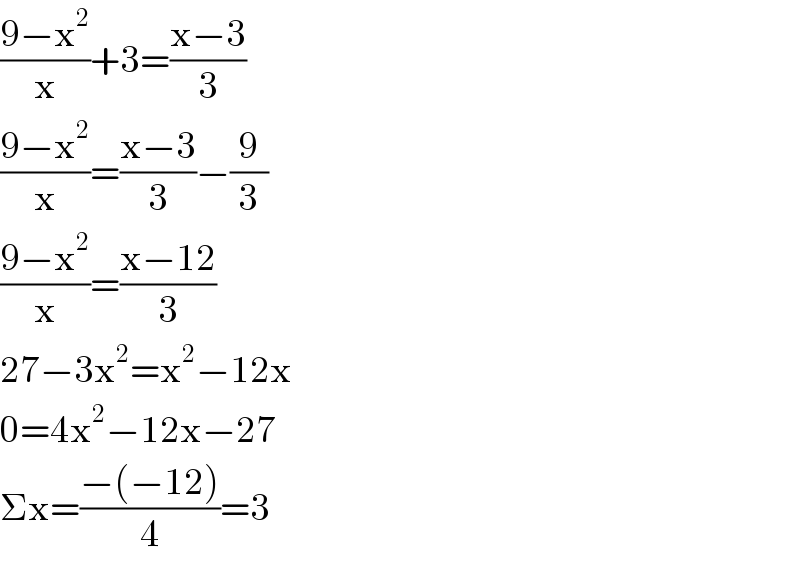
$$\frac{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}+\mathrm{3}=\frac{\mathrm{x}−\mathrm{3}}{\mathrm{3}} \\ $$$$\frac{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}=\frac{\mathrm{x}−\mathrm{3}}{\mathrm{3}}−\frac{\mathrm{9}}{\mathrm{3}} \\ $$$$\frac{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}=\frac{\mathrm{x}−\mathrm{12}}{\mathrm{3}} \\ $$$$\mathrm{27}−\mathrm{3x}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\mathrm{12x} \\ $$$$\mathrm{0}=\mathrm{4x}^{\mathrm{2}} −\mathrm{12x}−\mathrm{27} \\ $$$$\Sigma\mathrm{x}=\frac{−\left(−\mathrm{12}\right)}{\mathrm{4}}=\mathrm{3} \\ $$
