Question Number 74191 by Mr. K last updated on 20/Nov/19

$$\:\:\:\:\mathrm{9}{Y}\mathrm{4} \\ $$$$+\mathrm{75}{X} \\ $$$$\:\:\:\:{Z}\mathrm{86} \\ $$$$−−−− \\ $$$${W}\mathrm{387} \\ $$$${find}\:{X}+{Y}+{Z}+{W}. \\ $$
Answered by MJS last updated on 20/Nov/19
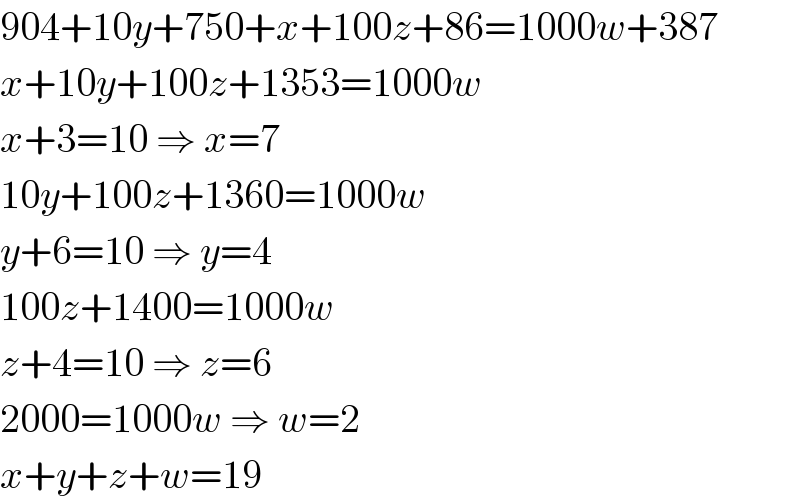
$$\mathrm{904}+\mathrm{10}{y}+\mathrm{750}+{x}+\mathrm{100}{z}+\mathrm{86}=\mathrm{1000}{w}+\mathrm{387} \\ $$$${x}+\mathrm{10}{y}+\mathrm{100}{z}+\mathrm{1353}=\mathrm{1000}{w} \\ $$$${x}+\mathrm{3}=\mathrm{10}\:\Rightarrow\:{x}=\mathrm{7} \\ $$$$\mathrm{10}{y}+\mathrm{100}{z}+\mathrm{1360}=\mathrm{1000}{w} \\ $$$${y}+\mathrm{6}=\mathrm{10}\:\Rightarrow\:{y}=\mathrm{4} \\ $$$$\mathrm{100}{z}+\mathrm{1400}=\mathrm{1000}{w} \\ $$$${z}+\mathrm{4}=\mathrm{10}\:\Rightarrow\:{z}=\mathrm{6} \\ $$$$\mathrm{2000}=\mathrm{1000}{w}\:\Rightarrow\:{w}=\mathrm{2} \\ $$$${x}+{y}+{z}+{w}=\mathrm{19} \\ $$
Commented by Mr. K last updated on 20/Nov/19

$${why}\:{x}+\mathrm{3}=\mathrm{10}? \\ $$
Commented by MJS last updated on 20/Nov/19

$$\mathrm{because}\:\mathrm{1353}\:\mathrm{has}\:\mathrm{to}\:\mathrm{get}\:\mathrm{1000}{w} \\ $$$$\mathrm{1353}+{zyx}=\mathrm{1000}{w} \\ $$$$\mathrm{1353} \\ $$$$\:\:^{\:\:} {zyx} \\ $$$$=== \\ $$$${w}\mathrm{000} \\ $$
Commented by malwaan last updated on 20/Nov/19
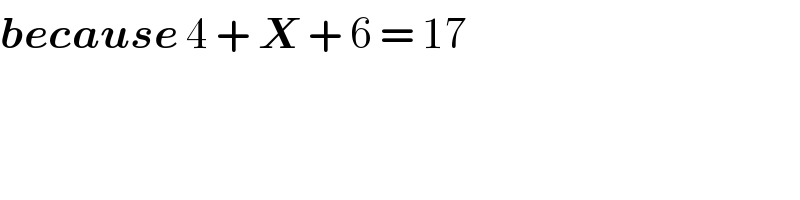
$$\boldsymbol{{because}}\:\mathrm{4}\:+\:\boldsymbol{{X}}\:+\:\mathrm{6}\:=\:\mathrm{17} \\ $$
Answered by MJS last updated on 20/Nov/19

$$\mathrm{09}{y}\mathrm{4} \\ $$$$\mathrm{075}{x} \\ $$$$\mathrm{0}{z}\mathrm{86} \\ $$$$=== \\ $$$${w}\mathrm{387} \\ $$$$ \\ $$$$\mathrm{same}\:\mathrm{as} \\ $$$$ \\ $$$$\mathrm{0904} \\ $$$$\mathrm{00}{y}\mathrm{0} \\ $$$$\mathrm{0750} \\ $$$$\mathrm{000}{x} \\ $$$$\mathrm{0086} \\ $$$$\mathrm{0}{z}\mathrm{00} \\ $$$$=== \\ $$$${w}\mathrm{387} \\ $$$$ \\ $$$$\mathrm{same}\:\mathrm{as} \\ $$$$ \\ $$$$\mathrm{1740} \\ $$$$\mathrm{0}{zyx} \\ $$$$=== \\ $$$${w}\mathrm{387} \\ $$$$ \\ $$$$\mathrm{sane}\:\mathrm{as} \\ $$$$ \\ $$$$\mathrm{1353} \\ $$$$\mathrm{0}{zyx} \\ $$$$=== \\ $$$${w}\mathrm{000} \\ $$$$ \\ $$$$\mathrm{same}\:\mathrm{as} \\ $$$$ \\ $$$$\:\:\:{w}\mathrm{000} \\ $$$$−\mathrm{1353} \\ $$$$==== \\ $$$$\:\:\:\:\:\mathrm{0}{zyx} \\ $$
