Question Number 1322 by 123456 last updated on 22/Jul/15
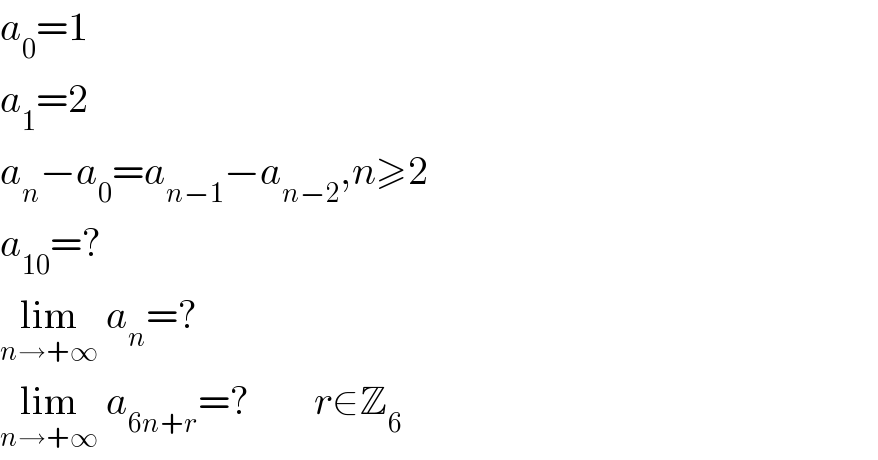
$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${a}_{\mathrm{1}} =\mathrm{2} \\ $$$${a}_{{n}} −{a}_{\mathrm{0}} ={a}_{{n}−\mathrm{1}} −{a}_{{n}−\mathrm{2}} ,{n}\geqslant\mathrm{2} \\ $$$${a}_{\mathrm{10}} =? \\ $$$$\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:{a}_{{n}} =? \\ $$$$\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:{a}_{\mathrm{6}{n}+{r}} =?\:\:\:\:\:\:\:\:{r}\in\mathbb{Z}_{\mathrm{6}} \\ $$
Commented by 112358 last updated on 22/Jul/15

$${a}_{\mathrm{2}} −\mathrm{1}={a}_{\mathrm{1}} −\mathrm{1}\Rightarrow{a}_{\mathrm{2}} =\mathrm{2} \\ $$$${a}_{\mathrm{3}} −\mathrm{1}=\mathrm{2}−\mathrm{2}\Rightarrow{a}_{\mathrm{3}} =\mathrm{1} \\ $$$${a}_{\mathrm{4}} −\mathrm{1}=\mathrm{1}−\mathrm{2}\Rightarrow{a}_{\mathrm{4}} =\mathrm{0} \\ $$$${a}_{\mathrm{5}} −\mathrm{1}=\mathrm{0}−\mathrm{1}\Rightarrow{a}_{\mathrm{5}} =\mathrm{0} \\ $$$${a}_{\mathrm{6}} −\mathrm{1}=\mathrm{0}−\mathrm{0}\Rightarrow{a}_{\mathrm{6}} =\mathrm{1} \\ $$$${a}_{\mathrm{7}} −\mathrm{1}=\mathrm{1}−\mathrm{0}\Rightarrow{a}_{\mathrm{7}} =\mathrm{2} \\ $$$${a}_{\mathrm{8}} −\mathrm{1}=\mathrm{2}−\mathrm{1}\Rightarrow{a}_{\mathrm{8}} =\mathrm{2} \\ $$$${a}_{\mathrm{9}} −\mathrm{1}=\mathrm{2}−\mathrm{2}\Rightarrow{a}_{\mathrm{9}} =\mathrm{1} \\ $$$${a}_{\mathrm{10}} −\mathrm{1}=\mathrm{1}−\mathrm{2}\Rightarrow{a}_{\mathrm{10}} =\mathrm{0} \\ $$$${Continuing}\:{with}\:{the}\:{terms}\:{for}\:{n}>\mathrm{10} \\ $$$${a}_{\mathrm{11}} −\mathrm{1}=\mathrm{0}−\mathrm{1}\Rightarrow{a}_{\mathrm{11}} =\mathrm{0} \\ $$$${a}_{\mathrm{12}} −\mathrm{1}=\mathrm{0}−\mathrm{0}\Rightarrow{a}_{\mathrm{12}} =\mathrm{1} \\ $$$${a}_{\mathrm{13}} −\mathrm{1}=\mathrm{1}−\mathrm{0}\Rightarrow{a}_{\mathrm{13}} =\mathrm{2} \\ $$$${a}_{\mathrm{14}} −\mathrm{1}=\mathrm{2}−\mathrm{1}\Rightarrow{a}_{\mathrm{14}} =\mathrm{2} \\ $$$${The}\:{pattern}\:{of}\:{the}\:{sequence} \\ $$$$\left\{{a}_{{n}} \right\}=\mathrm{1},\mathrm{2},\mathrm{2},\mathrm{1},\mathrm{0},\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{2},\mathrm{1},\mathrm{0},\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{2},… \\ $$$${is}\:{oscillatory}\:{and}\:{periodic}\:{but}\:{is}\:{not}\:{convergent}. \\ $$$${So}\underset{{n}\rightarrow+\infty} {\mathrm{lim}}{a}_{{n}} \:{is}\:{indeterminate}\:. \\ $$$$\left({Correct}\:{me}\:{if}\:{I}'{m}\:{wrong}.\right) \\ $$$$ \\ $$
Commented by 112358 last updated on 24/Jul/15

$${For}\:{l}=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}{a}_{\mathrm{6}{n}+{r}} \:,{r}\in\mathbb{Z}_{\mathrm{6}} \:{this}\:{limit} \\ $$$${is}\:{undefined}\:{since}\:{we}\:{cannot} \\ $$$${explicitly}\:{determine}\:{which}\:{value} \\ $$$${n}\:{takes}\:{at}\:+\infty\:\forall{r}\in\mathbb{Z}_{\mathrm{6}} .\:{We}\:{thus}\: \\ $$$${cannot}\:{be}\:{sure}\:{where}\:{along}\:{the}\: \\ $$$${sequence}\:{we}\:{are}\:{for}\:{any}\:{given}\: \\ $$$${value}\:{of}\:{r}\:{as}\:{n}\:{becomes}\:{arbitrarily} \\ $$$${large}. \\ $$
