Question Number 69954 by 20190927 last updated on 29/Sep/19

$$\mathrm{A}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\:\:\:\mathrm{find}\:\mathrm{A}^{\mathrm{n}} \\ $$
Commented by mathmax by abdo last updated on 29/Sep/19
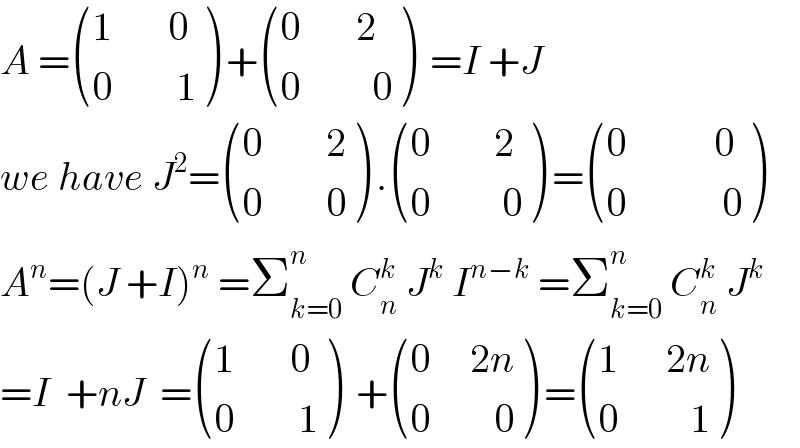
$${A}\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:+\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:\:={I}\:+{J} \\ $$$${we}\:{have}\:{J}^{\mathrm{2}} =\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:.\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$${A}^{{n}} =\left({J}\:+{I}\right)^{{n}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{J}^{{k}} \:{I}^{{n}−{k}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{J}^{{k}} \\ $$$$={I}\:\:+{nJ}\:\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\:+\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\mathrm{2}{n}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\mathrm{2}{n}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$
Commented by kaivan.ahmadi last updated on 29/Sep/19
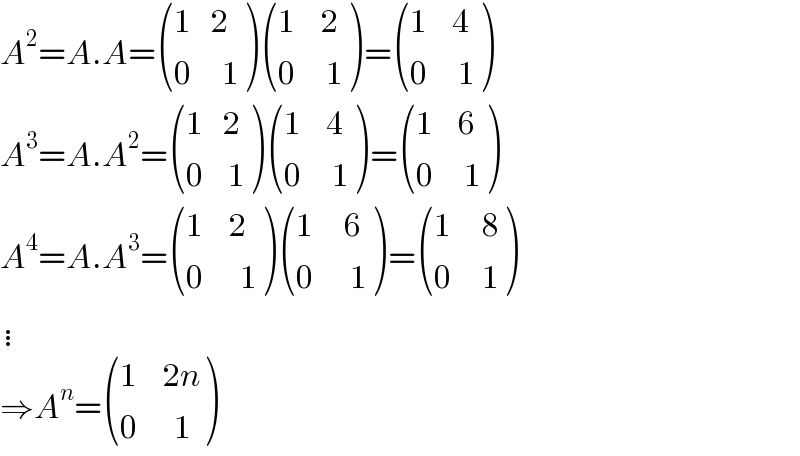
$${A}^{\mathrm{2}} ={A}.{A}=\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{4}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${A}^{\mathrm{3}} ={A}.{A}^{\mathrm{2}} =\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{4}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{6}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${A}^{\mathrm{4}} ={A}.{A}^{\mathrm{3}} =\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{6}}\\{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{8}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\vdots \\ $$$$\Rightarrow{A}^{{n}} =\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{2}{n}}\\{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$
Commented by 20190927 last updated on 29/Sep/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
