Question Number 10340 by konen last updated on 04/Feb/17
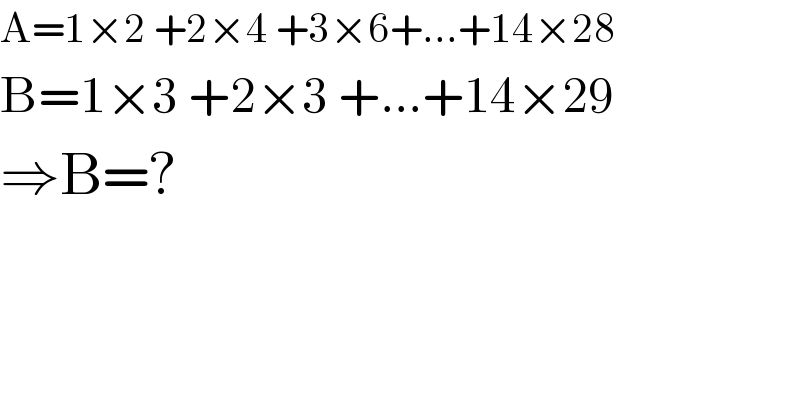
$$\mathrm{A}=\mathrm{1}×\mathrm{2}\:+\mathrm{2}×\mathrm{4}\:+\mathrm{3}×\mathrm{6}+…+\mathrm{14}×\mathrm{28} \\ $$$$\mathrm{B}=\mathrm{1}×\mathrm{3}\:+\mathrm{2}×\mathrm{3}\:+…+\mathrm{14}×\mathrm{29} \\ $$$$\Rightarrow\mathrm{B}=? \\ $$
Commented by mrW1 last updated on 04/Feb/17
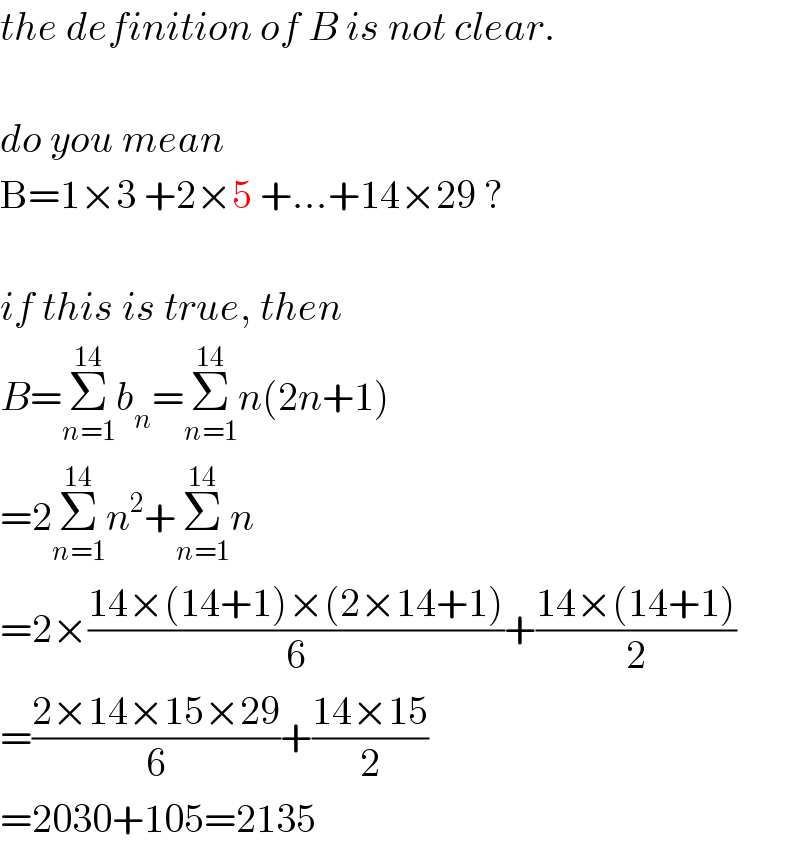
$${the}\:{definition}\:{of}\:{B}\:{is}\:{not}\:{clear}. \\ $$$$ \\ $$$${do}\:{you}\:{mean}\: \\ $$$$\mathrm{B}=\mathrm{1}×\mathrm{3}\:+\mathrm{2}×\mathrm{5}\:+…+\mathrm{14}×\mathrm{29}\:? \\ $$$$ \\ $$$${if}\:{this}\:{is}\:{true},\:{then} \\ $$$${B}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}{b}_{{n}} =\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}{n}\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}{n}^{\mathrm{2}} +\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}{n} \\ $$$$=\mathrm{2}×\frac{\mathrm{14}×\left(\mathrm{14}+\mathrm{1}\right)×\left(\mathrm{2}×\mathrm{14}+\mathrm{1}\right)}{\mathrm{6}}+\frac{\mathrm{14}×\left(\mathrm{14}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{2}×\mathrm{14}×\mathrm{15}×\mathrm{29}}{\mathrm{6}}+\frac{\mathrm{14}×\mathrm{15}}{\mathrm{2}} \\ $$$$=\mathrm{2030}+\mathrm{105}=\mathrm{2135} \\ $$
