Question Number 10347 by konen last updated on 04/Feb/17
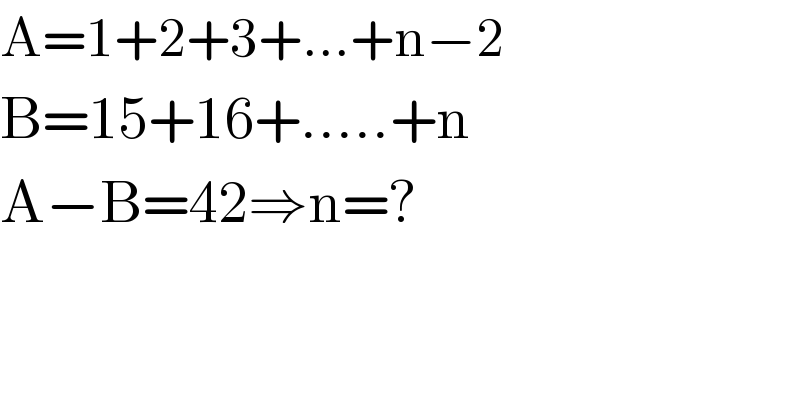
$$\mathrm{A}=\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{n}−\mathrm{2} \\ $$$$\mathrm{B}=\mathrm{15}+\mathrm{16}+…..+\mathrm{n} \\ $$$$\mathrm{A}−\mathrm{B}=\mathrm{42}\Rightarrow\mathrm{n}=? \\ $$
Answered by mrW1 last updated on 05/Feb/17

$${A}=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}{k}=\frac{\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right)}{\mathrm{2}}=\frac{{n}^{\mathrm{2}} −\mathrm{3}{n}+\mathrm{2}}{\mathrm{2}} \\ $$$${B}=\underset{{k}=\mathrm{15}} {\overset{{n}} {\sum}}{k}=\frac{\left({n}+\mathrm{15}\right)\left({n}−\mathrm{14}\right)}{\mathrm{2}}=\frac{{n}^{\mathrm{2}} +{n}−\mathrm{210}}{\mathrm{2}} \\ $$$${A}−{B}=\mathrm{42} \\ $$$$\frac{{n}^{\mathrm{2}} −\mathrm{3}{n}+\mathrm{2}−{n}^{\mathrm{2}} −{n}+\mathrm{210}}{\mathrm{2}}=\mathrm{42} \\ $$$$\frac{\mathrm{212}−\mathrm{4}{n}}{\mathrm{2}}=\mathrm{42} \\ $$$${n}=\frac{\mathrm{212}−\mathrm{84}}{\mathrm{4}}=\mathrm{32} \\ $$
Answered by arge last updated on 05/Feb/17
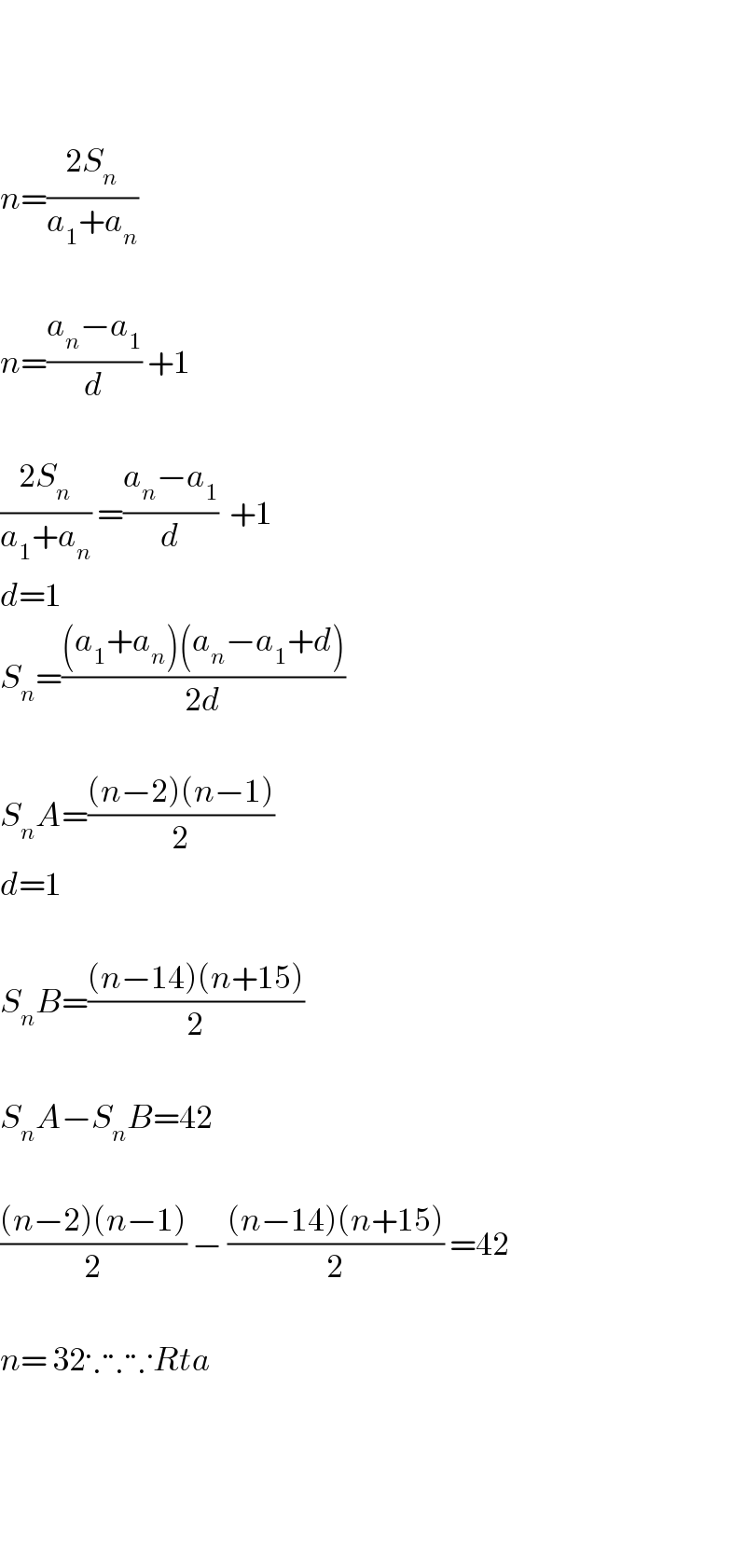
$$ \\ $$$$ \\ $$$$ \\ $$$${n}=\frac{\mathrm{2}{S}_{{n}} }{{a}_{\mathrm{1}} +{a}_{{n}} } \\ $$$$ \\ $$$${n}=\frac{{a}_{{n}} −{a}_{\mathrm{1}} }{{d}}\:+\mathrm{1} \\ $$$$ \\ $$$$\frac{\mathrm{2}{S}_{{n}} }{{a}_{\mathrm{1}} +{a}_{{n}} }\:=\frac{{a}_{{n}} −{a}_{\mathrm{1}} }{{d}}\:\:+\mathrm{1} \\ $$$${d}=\mathrm{1} \\ $$$${S}_{{n}} =\frac{\left({a}_{\mathrm{1}} +{a}_{{n}} \right)\left({a}_{{n}} −{a}_{\mathrm{1}} +{d}\right)}{\mathrm{2}{d}} \\ $$$$ \\ $$$${S}_{{n}} {A}=\frac{\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$${d}=\mathrm{1} \\ $$$$ \\ $$$${S}_{{n}} {B}=\frac{\left({n}−\mathrm{14}\right)\left({n}+\mathrm{15}\right)}{\mathrm{2}} \\ $$$$ \\ $$$${S}_{{n}} {A}−{S}_{{n}} {B}=\mathrm{42} \\ $$$$ \\ $$$$\frac{\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right)}{\mathrm{2}}\:−\:\frac{\left({n}−\mathrm{14}\right)\left({n}+\mathrm{15}\right)}{\mathrm{2}}\:=\mathrm{42} \\ $$$$ \\ $$$${n}=\:\mathrm{32}\because\because\because{Rta} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
