Question Number 4575 by FilupSmith last updated on 08/Feb/16
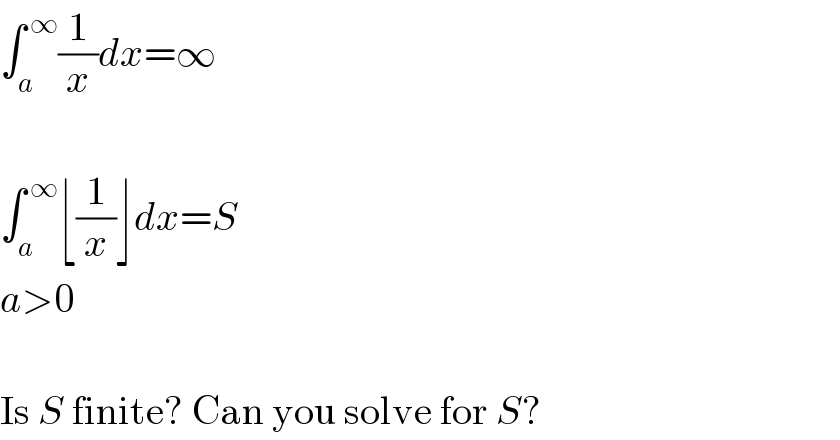
$$\int_{{a}} ^{\:\infty} \frac{\mathrm{1}}{{x}}{dx}=\infty \\ $$$$ \\ $$$$\int_{{a}} ^{\:\infty} \lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx}={S} \\ $$$${a}>\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Is}\:{S}\:\mathrm{finite}?\:\mathrm{Can}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{for}\:{S}? \\ $$
Commented by Yozzii last updated on 08/Feb/16

$${If}\:\mathrm{0}<{a}<\mathrm{1}\:{we}\:{have} \\ $$$${S}=\int_{{a}} ^{\infty} \lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx}=\int_{{a}} ^{\mathrm{1}} \lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx}+\int_{\mathrm{1}} ^{\infty} \lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx} \\ $$$${For}\:{all}\:{x}>\mathrm{1},\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{0}\Rightarrow\int_{\mathrm{1}} ^{\infty} \lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx}=\mathrm{0}. \\ $$$${For}\:\mathrm{0}<{a}\leqslant{x}\leqslant\mathrm{1}\Rightarrow\mathrm{1}\leqslant\frac{\mathrm{1}}{{x}}\leqslant\frac{\mathrm{1}}{{a}} \\ $$$$\therefore\:\underset{{a}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{1}}{{a}}=+\infty\Rightarrow\mathrm{1}\leqslant\lfloor\frac{\mathrm{1}}{{x}}\rfloor\leqslant\lfloor\frac{\mathrm{1}}{{a}}\rfloor\in\mathbb{Z}^{+} \\ $$$${So}\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor\:{takes}\:{all}\:{integral}\:{values}\:{from} \\ $$$$\mathrm{1}\:{to}\:\lfloor\frac{\mathrm{1}}{{a}}\rfloor\:{but}\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor\:{decreases}\:{as}\:{x}\:{goes} \\ $$$${from}\:{a}\:{to}\:\mathrm{1}.\:{S}\:{is}\:{finite}\:{since}\:{the}\: \\ $$$${integral}\:{S}=\int_{{a}} ^{\mathrm{1}} \lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx}\:{represents}\:{the} \\ $$$${total}\:{area}\:{of}\:{rectangles}\:{of}\:{height}\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor \\ $$$${and}\:{width}\:{d}={b}−{c}\:{such}\:{that}\:{for}\:{a}\:{given} \\ $$$${interval}\:{a}\leqslant{b}\leqslant{x}\leqslant{c}\leqslant\mathrm{1},\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor\:{is}\:{constant}. \\ $$$${For}\:{example}\:{if}\:{a}=\mathrm{0}.\mathrm{5}\Rightarrow{S}=\int_{\mathrm{0}.\mathrm{5}} ^{\mathrm{1}} \lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx}. \\ $$$$\therefore\:{For}\:\mathrm{0}.\mathrm{5}\leqslant{x}\leqslant\mathrm{1}\Rightarrow\mathrm{1}\leqslant\frac{\mathrm{1}}{{x}}\leqslant\mathrm{2} \\ $$$$\Rightarrow\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{1}.\:\underset{{x}\rightarrow\mathrm{0}.\mathrm{5}^{−} } {\mathrm{lim}}\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{2}\:{but}\:\underset{{x}\rightarrow\mathrm{0}.\mathrm{5}^{+} } {\mathrm{lim}}\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{1} \\ $$$${and}\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{1}\:{for}\:\mathrm{0}.\mathrm{5}<{x}\leqslant\mathrm{1}\:{since}\:\mathrm{1}\leqslant\frac{\mathrm{1}}{{x}}<\mathrm{2}. \\ $$$${Therefore},\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor\:{is}\:{undefined}\:{at}\:{x}=\mathrm{0}.\mathrm{5} \\ $$$${but}\:{graphically}\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{1}\:{for}\:\mathrm{0}.\mathrm{5}<{x}\leqslant\mathrm{1}. \\ $$$$\therefore\:{S}=\left({interval}\:{width}\right)\left({height}\right)=\left(\mathrm{1}−\mathrm{0}.\mathrm{5}\right)×\mathrm{1}=\mathrm{0}.\mathrm{5}. \\ $$$$ \\ $$$${In}\:{another}\:{example}\:{let}\:{a}=\mathrm{0}.\mathrm{0987}. \\ $$$$\Rightarrow\:{for}\:\mathrm{0}.\mathrm{0987}\leqslant{x}\leqslant\mathrm{1}\Rightarrow\mathrm{1}\leqslant\lfloor\frac{\mathrm{1}}{{x}}\rfloor\leqslant\mathrm{10} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzii last updated on 08/Feb/16
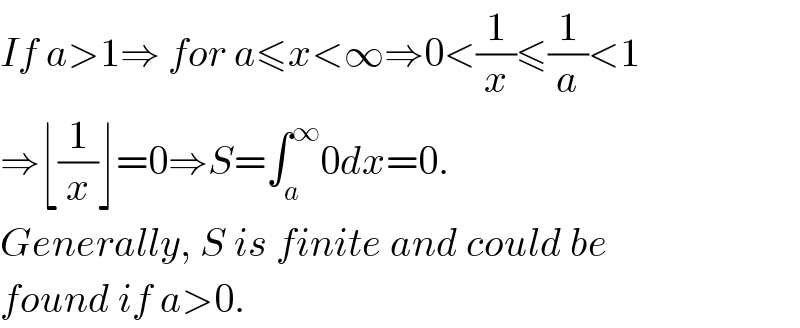
$${If}\:{a}>\mathrm{1}\Rightarrow\:{for}\:{a}\leqslant{x}<\infty\Rightarrow\mathrm{0}<\frac{\mathrm{1}}{{x}}\leqslant\frac{\mathrm{1}}{{a}}<\mathrm{1} \\ $$$$\Rightarrow\lfloor\frac{\mathrm{1}}{{x}}\rfloor=\mathrm{0}\Rightarrow{S}=\int_{{a}} ^{\infty} \mathrm{0}{dx}=\mathrm{0}. \\ $$$${Generally},\:{S}\:{is}\:{finite}\:{and}\:{could}\:{be}\: \\ $$$${found}\:{if}\:{a}>\mathrm{0}.\: \\ $$
