Question Number 5166 by 1771727373 last updated on 24/Apr/16
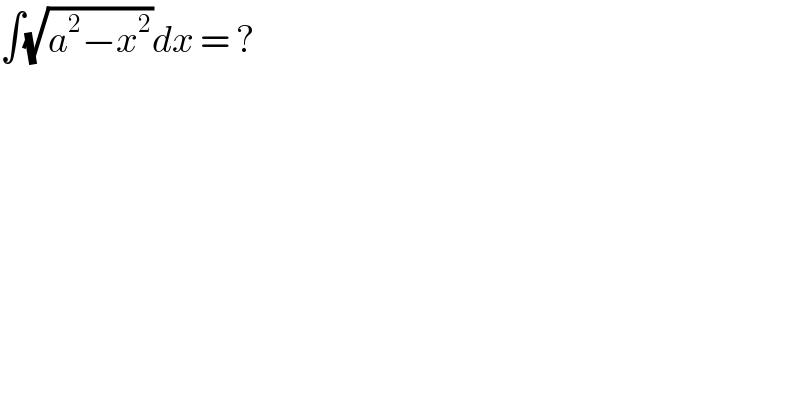
$$\int\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}\:=\:? \\ $$
Answered by 123456 last updated on 24/Apr/16
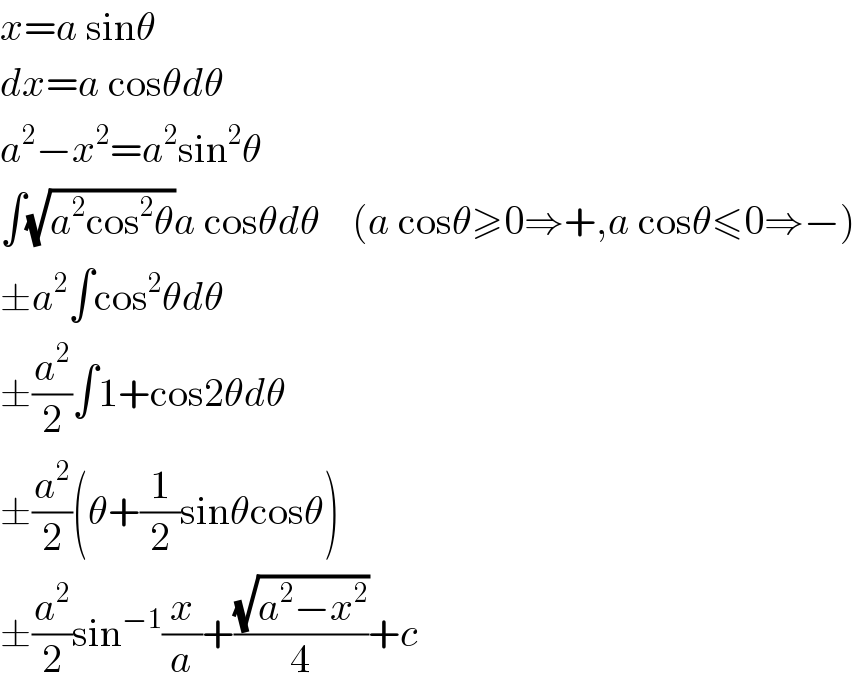
$${x}={a}\:\mathrm{sin}\theta \\ $$$${dx}={a}\:\mathrm{cos}\theta{d}\theta \\ $$$${a}^{\mathrm{2}} −{x}^{\mathrm{2}} ={a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta \\ $$$$\int\sqrt{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta}{a}\:\mathrm{cos}\theta{d}\theta\:\:\:\:\left({a}\:\mathrm{cos}\theta\geqslant\mathrm{0}\Rightarrow+,{a}\:\mathrm{cos}\theta\leqslant\mathrm{0}\Rightarrow−\right) \\ $$$$\pm{a}^{\mathrm{2}} \int\mathrm{cos}^{\mathrm{2}} \theta{d}\theta \\ $$$$\pm\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\int\mathrm{1}+\mathrm{cos2}\theta{d}\theta \\ $$$$\pm\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\theta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\theta\mathrm{cos}\theta\right) \\ $$$$\pm\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{{a}}+\frac{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{\mathrm{4}}+{c} \\ $$
