Question Number 11956 by Mahmoud A.R last updated on 07/Apr/17

$${A}\:,\:\mathrm{2}{B}\:,\mathrm{3}{C}\:,\mathrm{4}{D}\: \\ $$$${are}\:{positive}\:{numbers}\:{forming}\:{a}\: \\ $$$${geometric}\:{series}\: \\ $$$${prov}\:{that}\:: \\ $$$$\left({A}\:+\:\mathrm{3}{C}\right)\:\left({B}\:+\:\mathrm{2}{D}\right)\:>\:\mathrm{2} \\ $$
Commented by ajfour last updated on 07/Apr/17
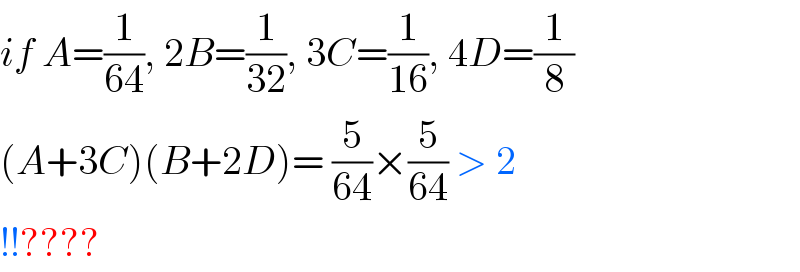
$${if}\:{A}=\frac{\mathrm{1}}{\mathrm{64}},\:\mathrm{2}{B}=\frac{\mathrm{1}}{\mathrm{32}},\:\mathrm{3}{C}=\frac{\mathrm{1}}{\mathrm{16}},\:\mathrm{4}{D}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\left({A}+\mathrm{3}{C}\right)\left({B}+\mathrm{2}{D}\right)=\:\frac{\mathrm{5}}{\mathrm{64}}×\frac{\mathrm{5}}{\mathrm{64}}\:>\:\mathrm{2}\: \\ $$$$!!???? \\ $$
Commented by FilupS last updated on 07/Apr/17
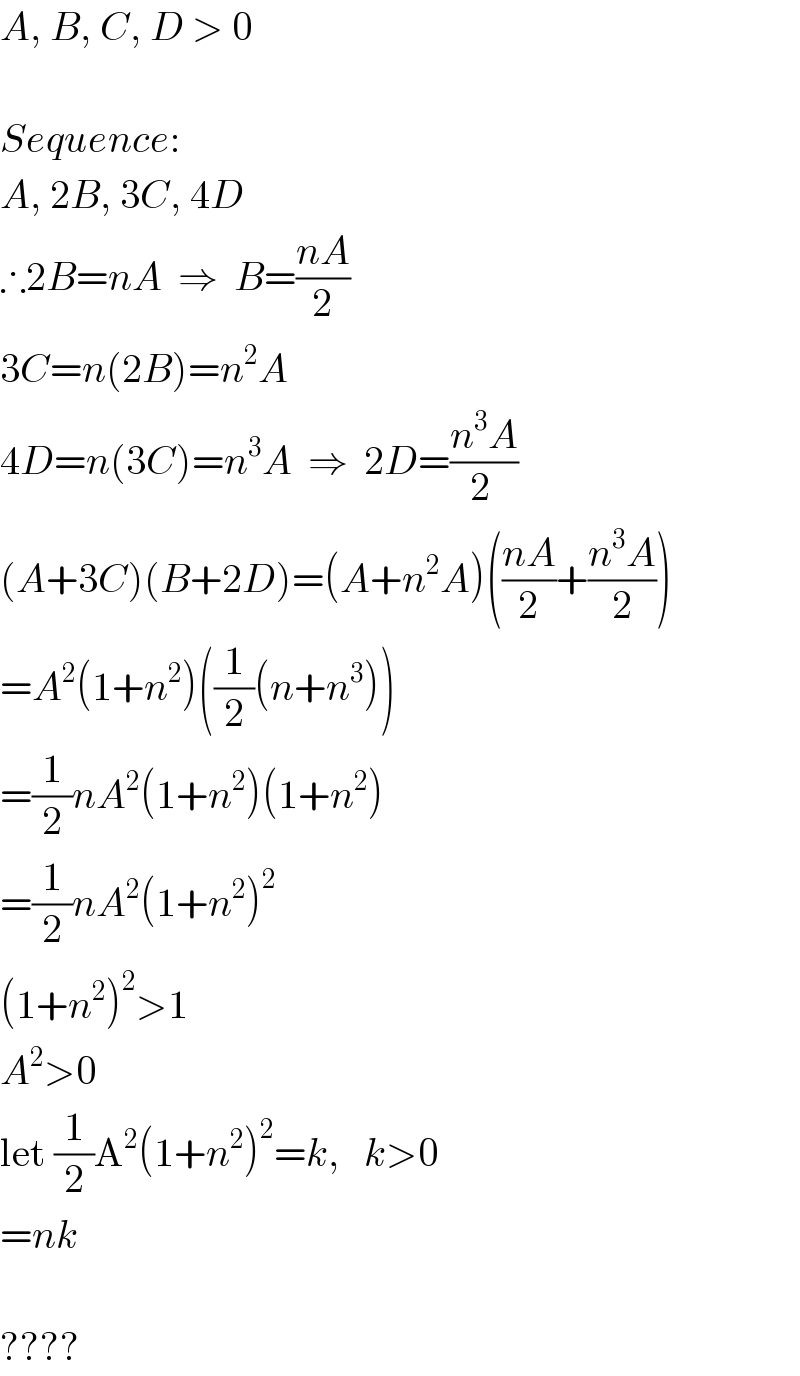
$${A},\:{B},\:{C},\:{D}\:>\:\mathrm{0} \\ $$$$\: \\ $$$${Sequence}: \\ $$$${A},\:\mathrm{2}{B},\:\mathrm{3}{C},\:\mathrm{4}{D} \\ $$$$\therefore\mathrm{2}{B}={nA}\:\:\Rightarrow\:\:{B}=\frac{{nA}}{\mathrm{2}} \\ $$$$\mathrm{3}{C}={n}\left(\mathrm{2}{B}\right)={n}^{\mathrm{2}} {A} \\ $$$$\mathrm{4}{D}={n}\left(\mathrm{3}{C}\right)={n}^{\mathrm{3}} {A}\:\:\Rightarrow\:\:\mathrm{2}{D}=\frac{{n}^{\mathrm{3}} {A}}{\mathrm{2}\:} \\ $$$$\left({A}+\mathrm{3}{C}\right)\left({B}+\mathrm{2}{D}\right)=\left({A}+{n}^{\mathrm{2}} {A}\right)\left(\frac{{nA}}{\mathrm{2}}+\frac{{n}^{\mathrm{3}} {A}}{\mathrm{2}}\right) \\ $$$$={A}^{\mathrm{2}} \left(\mathrm{1}+{n}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}}{\mathrm{2}}\left({n}+{n}^{\mathrm{3}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{nA}^{\mathrm{2}} \left(\mathrm{1}+{n}^{\mathrm{2}} \right)\left(\mathrm{1}+{n}^{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{nA}^{\mathrm{2}} \left(\mathrm{1}+{n}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{n}^{\mathrm{2}} \right)^{\mathrm{2}} >\mathrm{1} \\ $$$${A}^{\mathrm{2}} >\mathrm{0} \\ $$$$\mathrm{let}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{A}^{\mathrm{2}} \left(\mathrm{1}+{n}^{\mathrm{2}} \right)^{\mathrm{2}} ={k},\:\:\:{k}>\mathrm{0} \\ $$$$={nk} \\ $$$$ \\ $$$$???? \\ $$
