Question Number 137702 by SOMEDAVONG last updated on 05/Apr/21
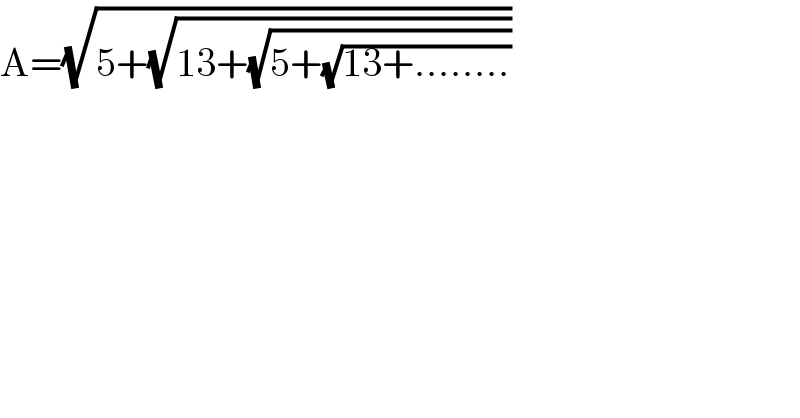
$$\mathrm{A}=\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+……..}}}} \\ $$
Answered by MJS_new last updated on 05/Apr/21
![A>(√5) (A^2 −5)^2 −13=A A^4 −10A^2 −A+12=0 (A−3)(A^3 +3A^2 −A−4)=0 A=3 [the 3^(rd) degree polynome has 3 real solutions <(√5)]](https://www.tinkutara.com/question/Q137718.png)
$${A}>\sqrt{\mathrm{5}} \\ $$$$\left({A}^{\mathrm{2}} −\mathrm{5}\right)^{\mathrm{2}} −\mathrm{13}={A} \\ $$$${A}^{\mathrm{4}} −\mathrm{10}{A}^{\mathrm{2}} −{A}+\mathrm{12}=\mathrm{0} \\ $$$$\left({A}−\mathrm{3}\right)\left({A}^{\mathrm{3}} +\mathrm{3}{A}^{\mathrm{2}} −{A}−\mathrm{4}\right)=\mathrm{0} \\ $$$${A}=\mathrm{3} \\ $$$$\left[\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{polynome}\:\mathrm{has}\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:<\sqrt{\mathrm{5}}\right] \\ $$
Answered by Dwaipayan Shikari last updated on 05/Apr/21
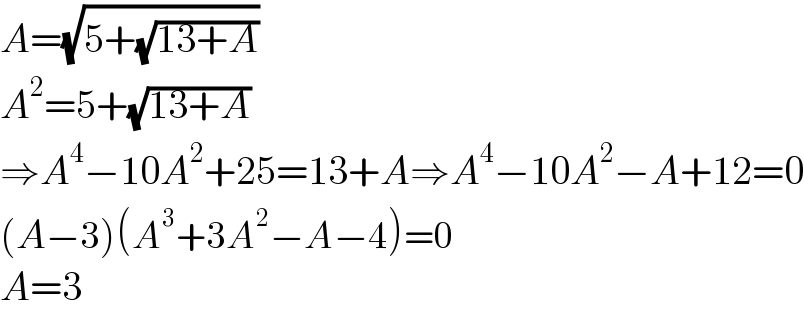
$${A}=\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+{A}}} \\ $$$${A}^{\mathrm{2}} =\mathrm{5}+\sqrt{\mathrm{13}+{A}} \\ $$$$\Rightarrow{A}^{\mathrm{4}} −\mathrm{10}{A}^{\mathrm{2}} +\mathrm{25}=\mathrm{13}+{A}\Rightarrow{A}^{\mathrm{4}} −\mathrm{10}{A}^{\mathrm{2}} −{A}+\mathrm{12}=\mathrm{0} \\ $$$$\left({A}−\mathrm{3}\right)\left({A}^{\mathrm{3}} +\mathrm{3}{A}^{\mathrm{2}} −{A}−\mathrm{4}\right)=\mathrm{0} \\ $$$${A}=\mathrm{3}\:\: \\ $$
