Question Number 77394 by jagoll last updated on 06/Jan/20
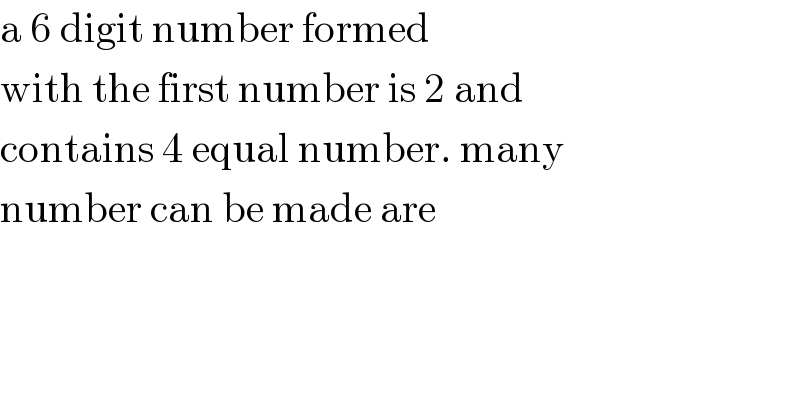
Commented by mr W last updated on 06/Jan/20

Commented by jagoll last updated on 06/Jan/20

Commented by jagoll last updated on 06/Jan/20
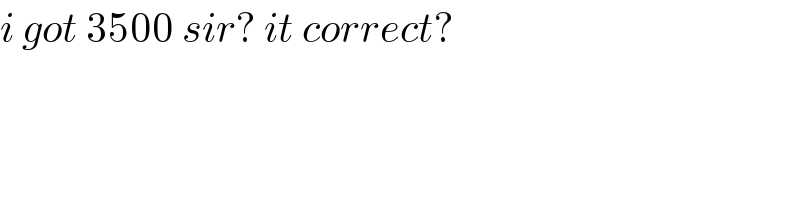
Commented by mr W last updated on 06/Jan/20
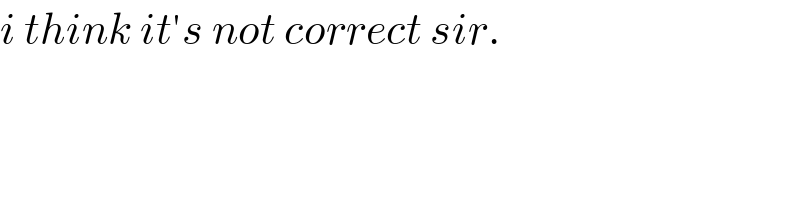
Answered by mr W last updated on 06/Jan/20
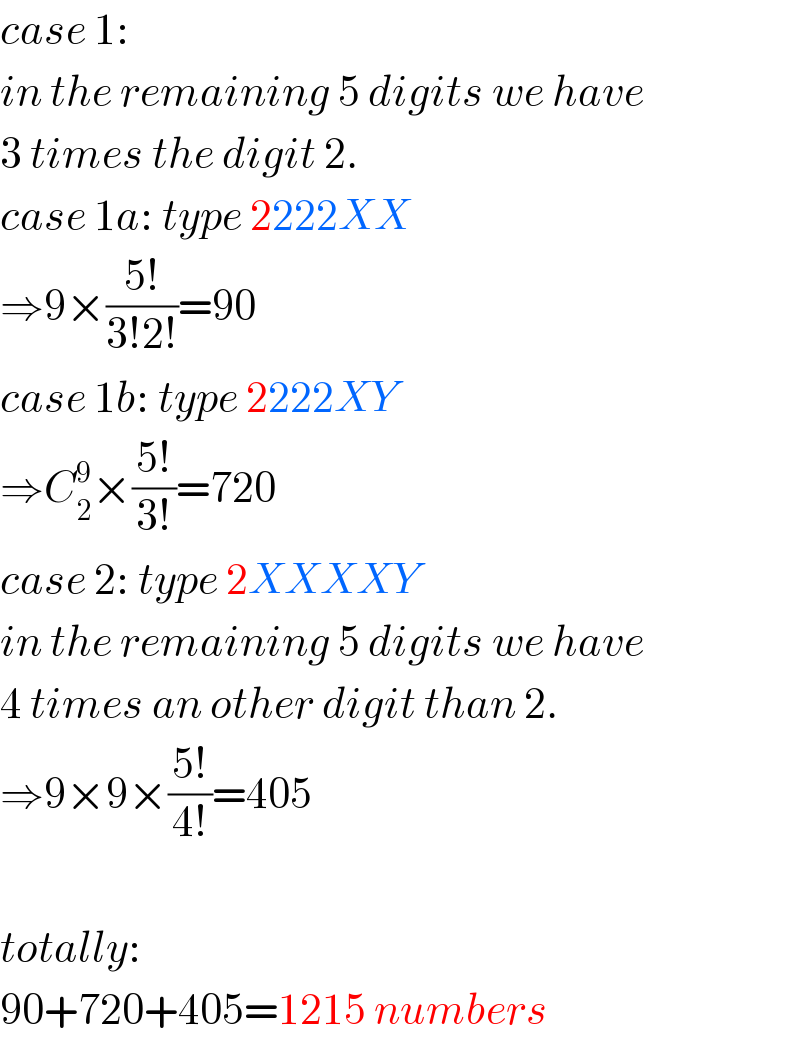
Commented by jagoll last updated on 06/Jan/20
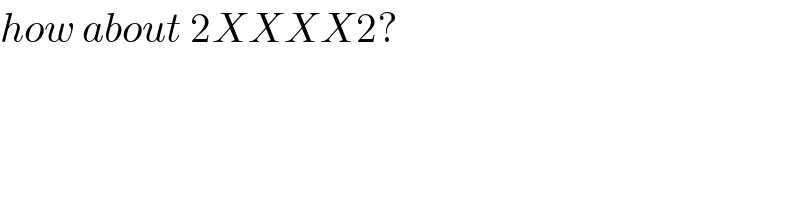
Commented by jagoll last updated on 06/Jan/20

Commented by mr W last updated on 06/Jan/20
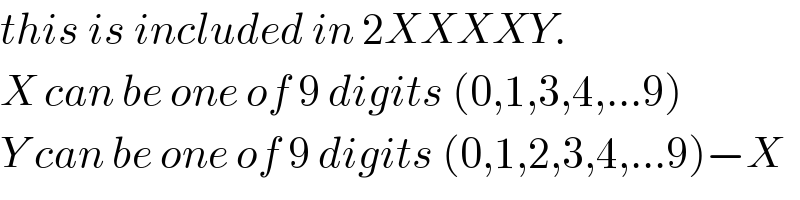
Commented by jagoll last updated on 06/Jan/20

Commented by jagoll last updated on 06/Jan/20
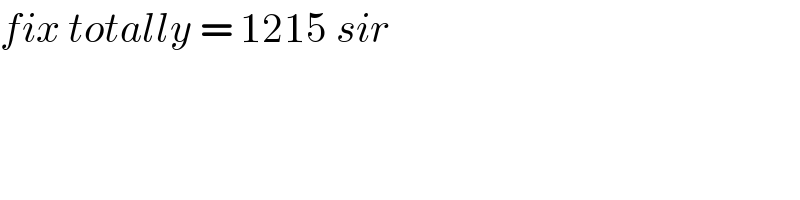
Commented by peter frank last updated on 06/Jan/20

