Question Number 71756 by aliesam last updated on 19/Oct/19
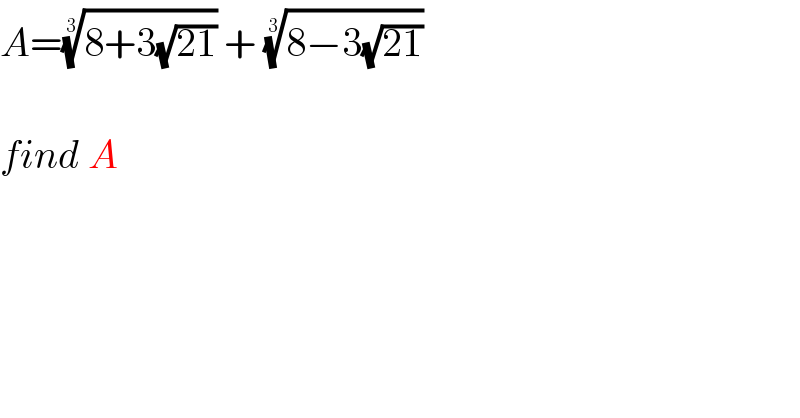
$${A}=\sqrt[{\mathrm{3}}]{\mathrm{8}+\mathrm{3}\sqrt{\mathrm{21}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{8}−\mathrm{3}\sqrt{\mathrm{21}}} \\ $$$$ \\ $$$${find}\:{A} \\ $$
Answered by MJS last updated on 19/Oct/19
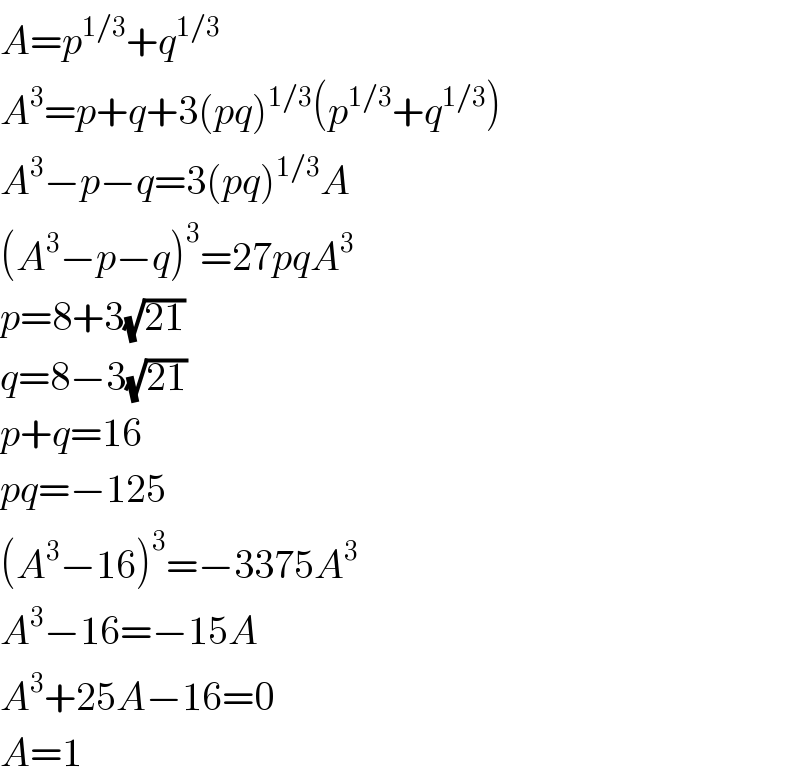
$${A}={p}^{\mathrm{1}/\mathrm{3}} +{q}^{\mathrm{1}/\mathrm{3}} \\ $$$${A}^{\mathrm{3}} ={p}+{q}+\mathrm{3}\left({pq}\right)^{\mathrm{1}/\mathrm{3}} \left({p}^{\mathrm{1}/\mathrm{3}} +{q}^{\mathrm{1}/\mathrm{3}} \right) \\ $$$${A}^{\mathrm{3}} −{p}−{q}=\mathrm{3}\left({pq}\right)^{\mathrm{1}/\mathrm{3}} {A} \\ $$$$\left({A}^{\mathrm{3}} −{p}−{q}\right)^{\mathrm{3}} =\mathrm{27}{pqA}^{\mathrm{3}} \\ $$$${p}=\mathrm{8}+\mathrm{3}\sqrt{\mathrm{21}} \\ $$$${q}=\mathrm{8}−\mathrm{3}\sqrt{\mathrm{21}} \\ $$$${p}+{q}=\mathrm{16} \\ $$$${pq}=−\mathrm{125} \\ $$$$\left({A}^{\mathrm{3}} −\mathrm{16}\right)^{\mathrm{3}} =−\mathrm{3375}{A}^{\mathrm{3}} \\ $$$${A}^{\mathrm{3}} −\mathrm{16}=−\mathrm{15}{A} \\ $$$${A}^{\mathrm{3}} +\mathrm{25}{A}−\mathrm{16}=\mathrm{0} \\ $$$${A}=\mathrm{1} \\ $$
Commented by aliesam last updated on 19/Oct/19

$${god}\:{bless}\:{you}\:{sir} \\ $$
