Question Number 10102 by konen last updated on 23/Jan/17
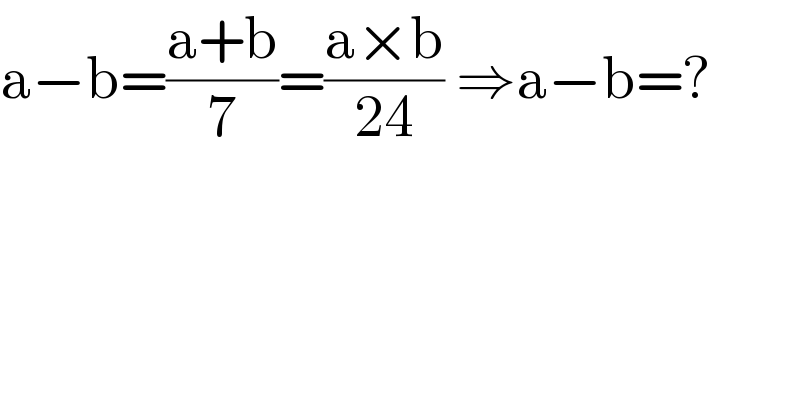
$$\mathrm{a}−\mathrm{b}=\frac{\mathrm{a}+\mathrm{b}}{\mathrm{7}}=\frac{\mathrm{a}×\mathrm{b}}{\mathrm{24}}\:\Rightarrow\mathrm{a}−\mathrm{b}=? \\ $$
Answered by mrW1 last updated on 23/Jan/17
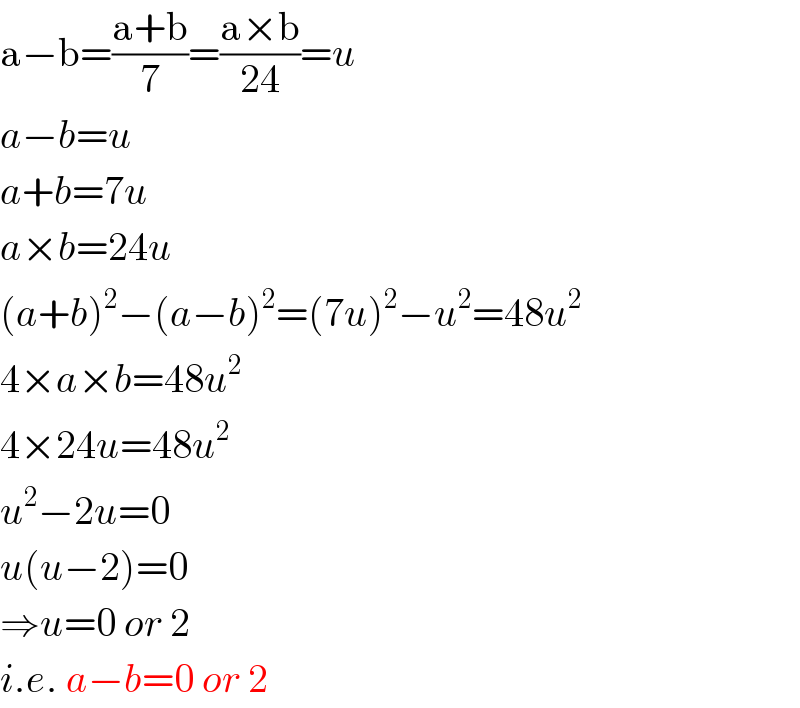
$$\mathrm{a}−\mathrm{b}=\frac{\mathrm{a}+\mathrm{b}}{\mathrm{7}}=\frac{\mathrm{a}×\mathrm{b}}{\mathrm{24}}={u} \\ $$$${a}−{b}={u} \\ $$$${a}+{b}=\mathrm{7}{u} \\ $$$${a}×{b}=\mathrm{24}{u} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} =\left(\mathrm{7}{u}\right)^{\mathrm{2}} −{u}^{\mathrm{2}} =\mathrm{48}{u}^{\mathrm{2}} \\ $$$$\mathrm{4}×{a}×{b}=\mathrm{48}{u}^{\mathrm{2}} \\ $$$$\mathrm{4}×\mathrm{24}{u}=\mathrm{48}{u}^{\mathrm{2}} \\ $$$${u}^{\mathrm{2}} −\mathrm{2}{u}=\mathrm{0} \\ $$$${u}\left({u}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{u}=\mathrm{0}\:{or}\:\mathrm{2} \\ $$$${i}.{e}.\:{a}−{b}=\mathrm{0}\:{or}\:\mathrm{2} \\ $$
Answered by arge last updated on 24/Jan/17
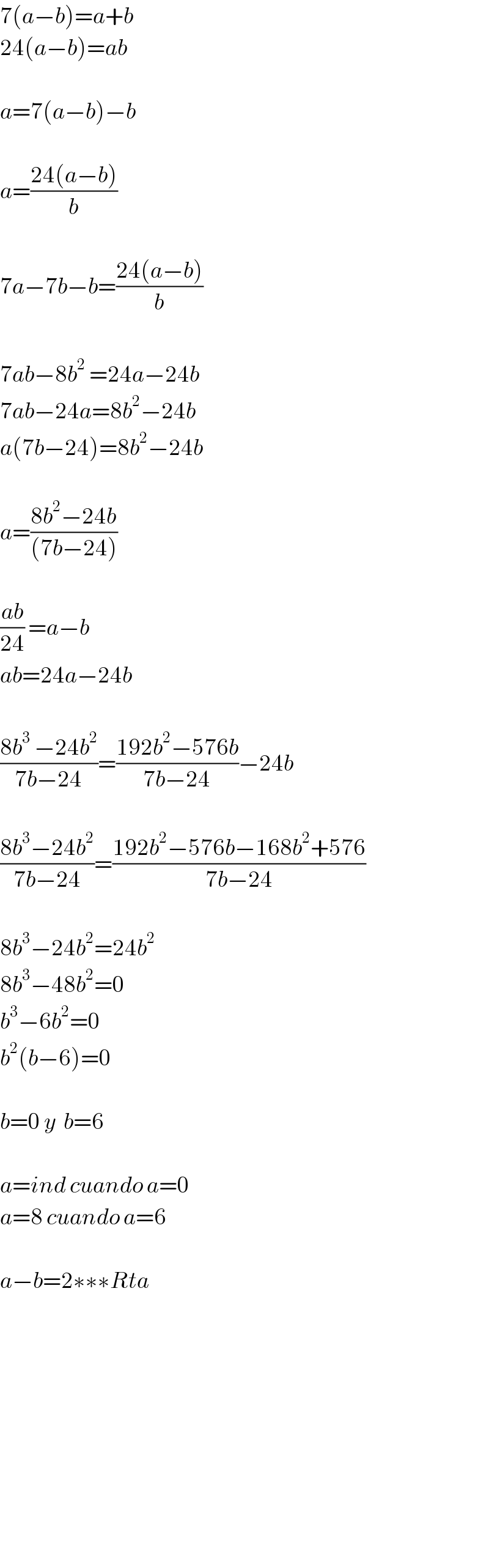
$$\mathrm{7}\left({a}−{b}\right)={a}+{b} \\ $$$$\mathrm{24}\left({a}−{b}\right)={ab} \\ $$$$ \\ $$$${a}=\mathrm{7}\left({a}−{b}\right)−{b} \\ $$$$ \\ $$$${a}=\frac{\mathrm{24}\left({a}−{b}\right)}{{b}} \\ $$$$ \\ $$$$\mathrm{7}{a}−\mathrm{7}{b}−{b}=\frac{\mathrm{24}\left({a}−{b}\right)}{{b}} \\ $$$$ \\ $$$$\mathrm{7}{ab}−\mathrm{8}{b}^{\mathrm{2}^{} } =\mathrm{24}{a}−\mathrm{24}{b} \\ $$$$\mathrm{7}{ab}−\mathrm{24}{a}=\mathrm{8}{b}^{\mathrm{2}} −\mathrm{24}{b} \\ $$$${a}\left(\mathrm{7}{b}−\mathrm{24}\right)=\mathrm{8}{b}^{\mathrm{2}} −\mathrm{24}{b} \\ $$$$ \\ $$$${a}=\frac{\mathrm{8}{b}^{\mathrm{2}} −\mathrm{24}{b}}{\left(\mathrm{7}{b}−\mathrm{24}\right)} \\ $$$$ \\ $$$$\frac{{ab}}{\mathrm{24}}\:={a}−{b} \\ $$$${ab}=\mathrm{24}{a}−\mathrm{24}{b} \\ $$$$ \\ $$$$\frac{\mathrm{8}{b}^{\mathrm{3}^{} } −\mathrm{24}{b}^{\mathrm{2}} }{\mathrm{7}{b}−\mathrm{24}}=\frac{\mathrm{192}{b}^{\mathrm{2}} −\mathrm{576}{b}}{\mathrm{7}{b}−\mathrm{24}}−\mathrm{24}{b} \\ $$$$ \\ $$$$\frac{\mathrm{8}{b}^{\mathrm{3}} −\mathrm{24}{b}^{\mathrm{2}} }{\mathrm{7}{b}−\mathrm{24}}=\frac{\mathrm{192}{b}^{\mathrm{2}} −\mathrm{576}{b}−\mathrm{168}{b}^{\mathrm{2}} +\mathrm{576}}{\mathrm{7}{b}−\mathrm{24}} \\ $$$$ \\ $$$$\mathrm{8}{b}^{\mathrm{3}} −\mathrm{24}{b}^{\mathrm{2}} =\mathrm{24}{b}^{\mathrm{2}} \\ $$$$\mathrm{8}{b}^{\mathrm{3}} −\mathrm{48}{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${b}^{\mathrm{3}} −\mathrm{6}{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${b}^{\mathrm{2}} \left({b}−\mathrm{6}\right)=\mathrm{0} \\ $$$$ \\ $$$${b}=\mathrm{0}\:{y}\:\:{b}=\mathrm{6} \\ $$$$ \\ $$$${a}={ind}\:{cuando}\:{a}=\mathrm{0} \\ $$$${a}=\mathrm{8}\:{cuando}\:{a}=\mathrm{6} \\ $$$$ \\ $$$${a}−{b}=\mathrm{2}\ast\ast\ast{Rta} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
