Question Number 11753 by Joel576 last updated on 31/Mar/17
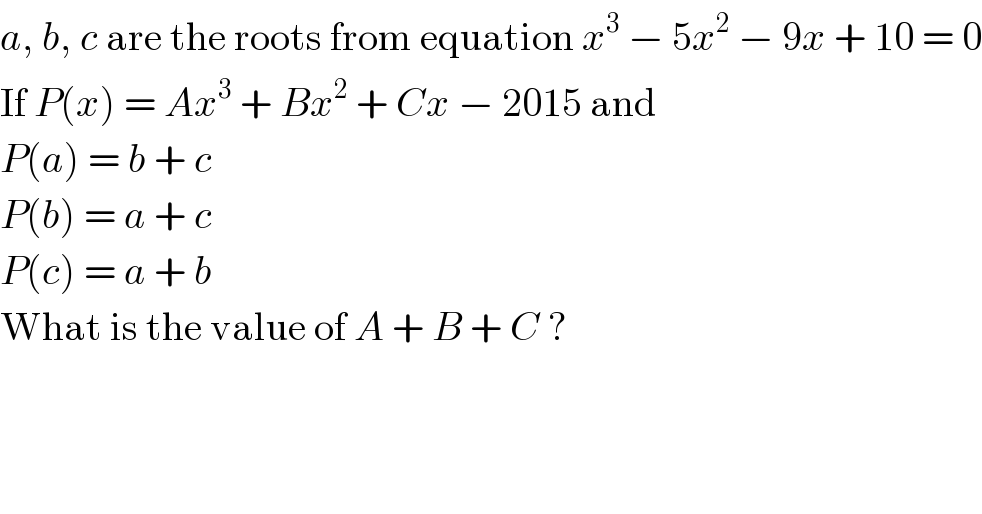
Answered by sma3l2996 last updated on 31/Mar/17

Commented by sma3l2996 last updated on 31/Mar/17

Commented by Joel576 last updated on 01/Apr/17
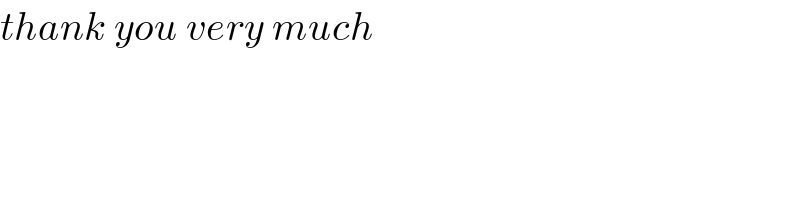
Answered by ajfour last updated on 31/Mar/17

Commented by ajfour last updated on 31/Mar/17
![As a,b, c are roots of x^3 −5x^2 −9x+10=0 or (x+2)(x^2 −7x+5) =0 are x=−2 , ((7±(√(29)))/2) we take a=−2; b+c=7; bc=((49−29)/4)= 5 ; a+b+c=5 . P(a)=b+c=Aa^3 +Ba^2 +Ca−2015 7=−8A+4B−2C−2015 .....(i) P(b)=a+c=Ab^3 +Bb^2 +Cb−2015 P(c)=a+b=Ac^3 +Bc^2 +Cc−2015 P(b)−P(c) gives b−c= (b−c)[A(b^2 +bc+c^2 ) +B(b+c)+C ] so, A[(b+c)^2 −bc] +B(b+c)+C=−1 ......(1) 44A+7B+C=−1 .....(ii) similarly [P(a)−P(b)]/(a−b) yields A(a^2 +ab+b^2 )+B(a+b)+C=−1 ......(2) and [P(c)−P(a)]/(c−a) gives A(c^2 +ac+a^2 )+B(c+a)+C=−1 ......(3) Adding eqns (1), (2), and (3) A{ 2(a^2 +b^2 +c^2 )+(ab+bc+ca)} +2B(a+b+c)+3C=−3 A{2(a+b+c)^2 −3(ab+bc+ca)} +2B(a+b+c)+3C=−3 or A{50−3(−9)}+10B+3C=−3 or 77A+10B+3C=−3 ...(iii) solving (i), (ii), and (iii) I found A+B+C = 2625 .](https://www.tinkutara.com/question/Q11785.png)
Commented by Joel576 last updated on 01/Apr/17

