a-b-c-b-a-c-c-a-b-a-b-c-12-b-c-a-c-a-b-

Question Number 142740 by mathdanisur last updated on 04/Jun/21

\frac{a}{b + c} = \frac{b}{a + c} = \frac{c}{a + b}; a \cdot b \cdot c = 12

(b + c) \cdot (a + c) \cdot (a + b) = ?

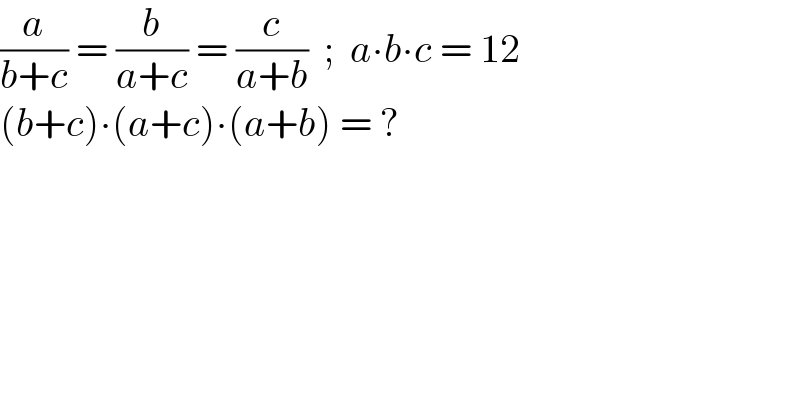
Commented by MJS_new last updated on 05/Jun/21

I found 2 possibilities

(1) a = b = c = \sqrt[3]{12} \Rightarrow answer is 96

(2) a < b < c \Rightarrow a = - \sqrt[3]{96} \land b = \sqrt[3]{12} - \sqrt[6]{486} \land c = \sqrt[3]{12} + \sqrt[6]{486} \Rightarrow answer is - 12

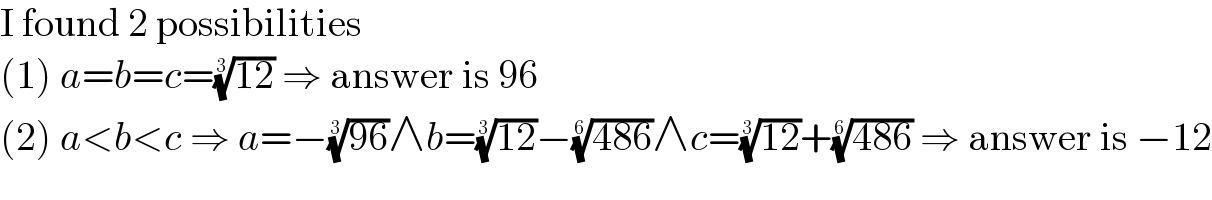
Commented by iloveisrael last updated on 05/Jun/21

y e s \dots i g o t 2 p o s s i b i l i t i e s

Commented by mathdanisur last updated on 05/Jun/21

t h a n k s s i r

Answered by Olaf_Thorendsen last updated on 05/Jun/21

\frac{a}{b + c} = \frac{b}{c + a} = \frac{c}{a + b}

\Rightarrow \frac{b + c}{a} = \frac{c + a}{b} = \frac{a + b}{c} (1)

Let s = a + b + c

(1) : \frac{s - a}{a} = \frac{s - b}{b} = \frac{s - c}{c}

\Rightarrow \frac{s}{a} = \frac{s}{b} = \frac{s}{c}

\frac{1}{a} = \frac{1}{b} = \frac{1}{c}

\Rightarrow a = b = c

a b c = 12 = a^{3} = b^{3} = c^{3}

(b + c) (a + c) (a + b) = {(2 a)}^{3} = 8 a^{3} = 96

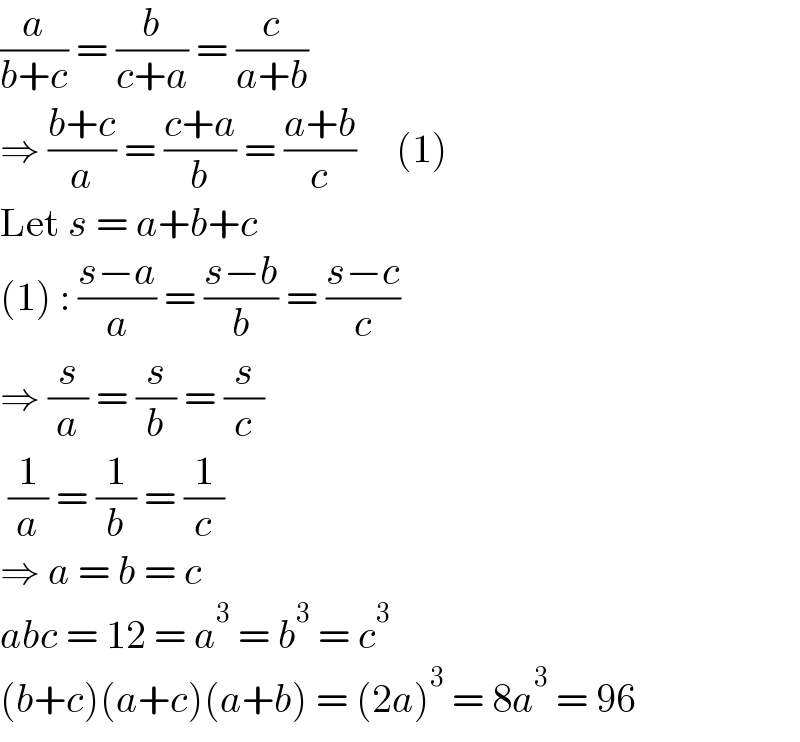
Commented by mathdanisur last updated on 05/Jun/21

t h a n k s s i r

Answered by iloveisrael last updated on 05/Jun/21

G i v e n a \times b \times c = 12 a n d

\frac{a}{b + c} = \frac{b}{a + c} = \frac{c}{a + b} t h e n

(b + c) (a + c) (a + b) = ?

l e t \frac{a}{b + c} = k \Rightarrow {\begin{cases} a = k (b + c) \\ b = k (a + c) \\ c = k (a + b) \end{cases}

\Rightarrow a + b + c = k (2 a + 2 b + 2 c)

\Rightarrow (a + b + c) (1 - 2 k) = 0

\Rightarrow a + b + c = 0 o r k = \frac{1}{2}

f o r k = \frac{1}{2}

\to a b c = {(\frac{1}{2})}^{3} (b + c) (a + c) (a + b)

\Rightarrow (b + c) (a + c) (a + b) = 12 \times 8 = 96

f o r a = - (b + c)

\Rightarrow \frac{b}{a + c} = \frac{c}{a + b} = - 1

\Rightarrow a + c = - b \land a + b = - c

t h e n (b + c) (a + c) (a + b) = (- a) (- b) (- c)

= - a b c = - 12

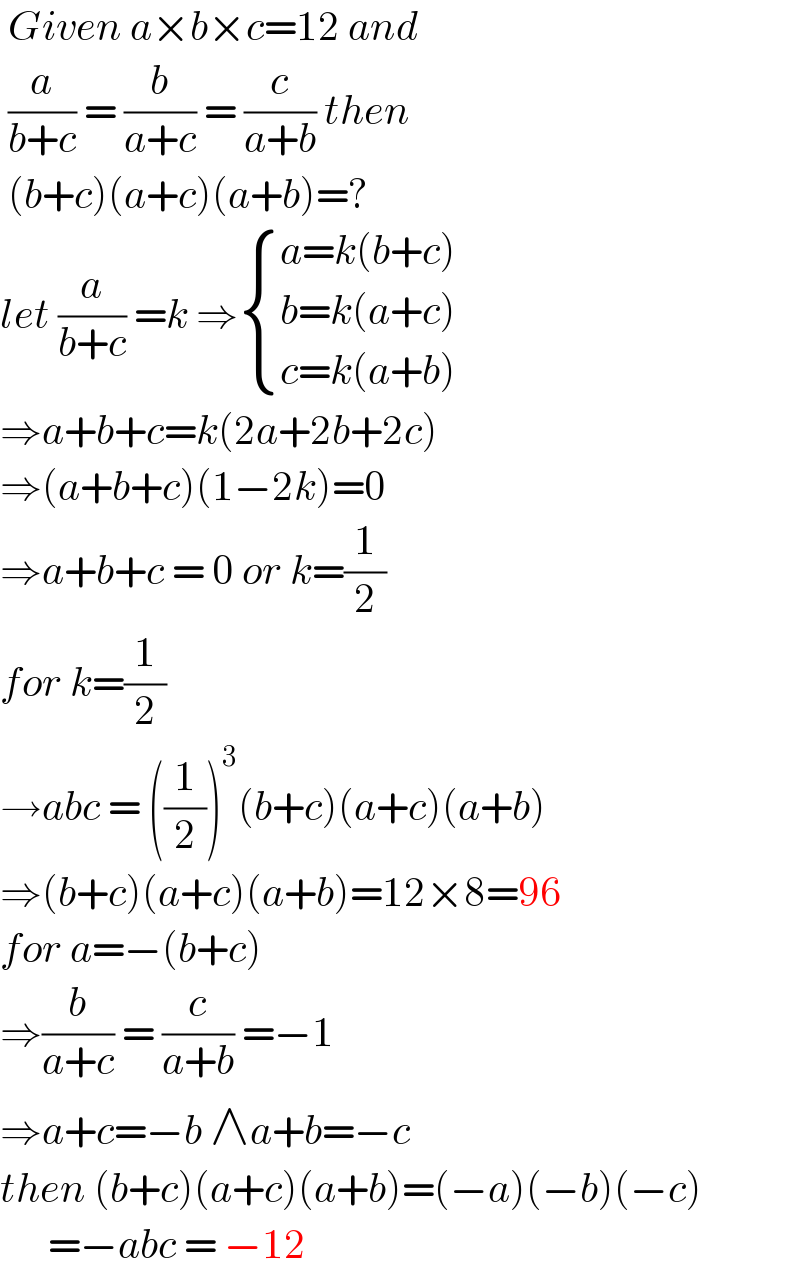
Commented by mathdanisur last updated on 05/Jun/21

t h a n k s s i r

Answered by 1549442205PVT last updated on 05/Jun/21

\frac{a}{b + c} = \frac{b}{c + a} = \frac{c}{a + b} = \frac{a + b + c}{a + b + b + c + c + a} = \frac{1}{2}

\Rightarrow \frac{a}{b + c} . \frac{b}{c + a} . \frac{c}{a + b} = {(\frac{1}{2})}^{3} = \frac{1}{8}

\Rightarrow (a + b) (b + c) (c + a) = 8 abc = 8.12 = 96

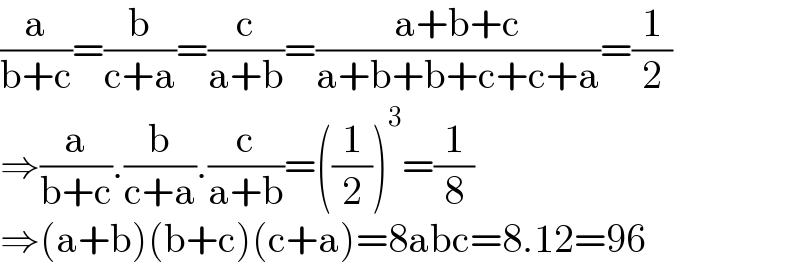
Commented by mathdanisur last updated on 05/Jun/21

t h a n k s s i r