Question Number 4795 by 123456 last updated on 13/Mar/16

$${a},{b},{c}\in\mathbb{C} \\ $$$${x}_{\mathrm{0}} ={a} \\ $$$${y}_{\mathrm{0}} ={b} \\ $$$${z}_{\mathrm{0}} ={c} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} −{y}_{{n}} \\ $$$${y}_{{n}+\mathrm{1}} ={y}_{{n}} −{z}_{{n}} \\ $$$${z}_{{n}+\mathrm{1}} ={z}_{{n}} −{x}_{{n}} \\ $$$${x}_{{n}} +{y}_{{n}} +{z}_{{n}} =?,{n}\geqslant\mathrm{1} \\ $$
Answered by Yozzii last updated on 13/Mar/16

$${Adding}\:{the}\:{three}\:{recurrence}\:{equations} \\ $$$${we}\:{obtain}\: \\ $$$${x}_{{n}+\mathrm{1}} +{y}_{{n}+\mathrm{1}} +{z}_{{n}+\mathrm{1}} ={x}_{{n}} −{y}_{{n}} +{y}_{{n}} −{z}_{{n}} +{z}_{{n}} −{x}_{{n}} =\mathrm{0}. \\ $$$$\Rightarrow{x}_{{n}} +{y}_{{n}} +{z}_{{n}} =\mathrm{0}\:{for}\:{all}\:{n}\in\mathbb{N}.\:\left(\ast\right) \\ $$$${Corollary}:\:{Since}\:{x}_{\mathrm{0}} ={a},\:{y}_{\mathrm{0}} ={b},\:{z}_{\mathrm{0}} ={c} \\ $$$$\Rightarrow\:{a}+{b}+{c}=\mathrm{0}\:{from}\:\left(\ast\right)\:{where}\:{a},{b},{c}\in\mathbb{C}. \\ $$$${Indeed},\:\exists{a},{b},{c}\in\mathbb{C}\:{such}\:{that}\:{a}+{b}+{c}=\mathrm{0}. \\ $$$${E}.{g}\:{a}=−\mathrm{1},{b}=\mathrm{3},\:{c}=−\mathrm{2}\:{or}\:{a}=\mathrm{1},{b}={e}^{\mathrm{2}\pi{i}/\mathrm{3}} ,{c}={e}^{−\mathrm{2}\pi{i}/\mathrm{3}} . \\ $$
Commented by prakash jain last updated on 13/Mar/16
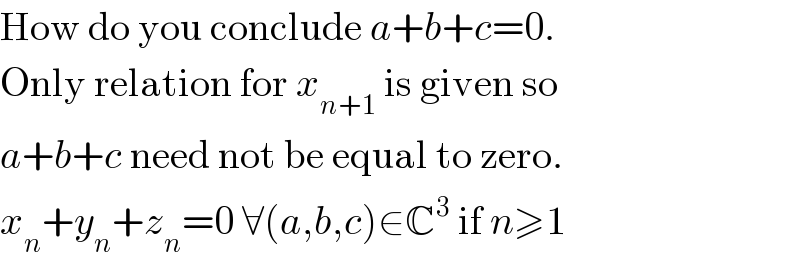
$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{conclude}\:{a}+{b}+{c}=\mathrm{0}. \\ $$$$\mathrm{Only}\:\mathrm{relation}\:\mathrm{for}\:{x}_{{n}+\mathrm{1}} \:\mathrm{is}\:\mathrm{given}\:\mathrm{so}\: \\ $$$${a}+{b}+{c}\:\mathrm{need}\:\mathrm{not}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{zero}. \\ $$$${x}_{{n}} +{y}_{{n}} +{z}_{{n}} =\mathrm{0}\:\forall\left({a},{b},{c}\right)\in\mathbb{C}^{\mathrm{3}} \:\mathrm{if}\:{n}\geqslant\mathrm{1} \\ $$
Commented by Yozzii last updated on 13/Mar/16
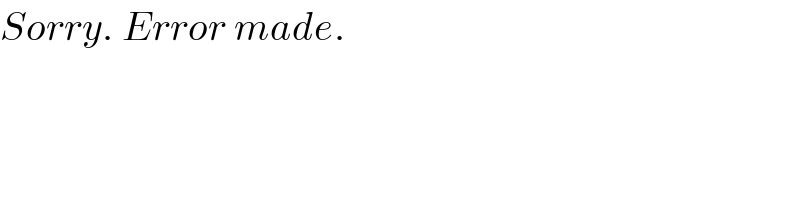
$${Sorry}.\:{Error}\:{made}. \\ $$$$ \\ $$
