Question Number 70051 by Aditya789 last updated on 30/Sep/19
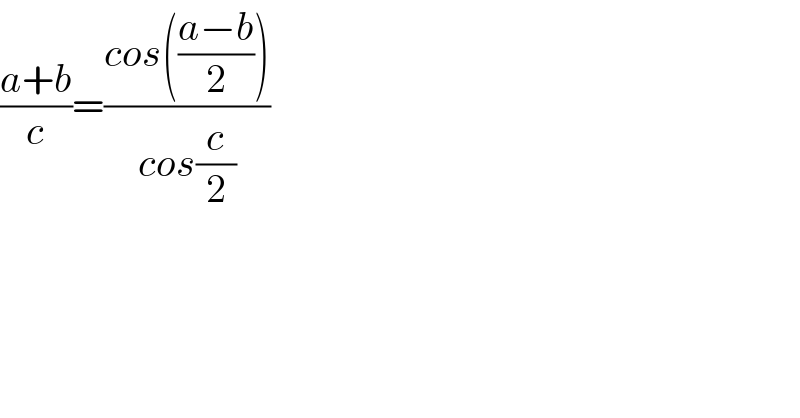
$$\frac{{a}+{b}}{{c}}=\frac{{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right)}{{cos}\frac{{c}}{\mathrm{2}}} \\ $$
Answered by $@ty@m123 last updated on 01/Oct/19
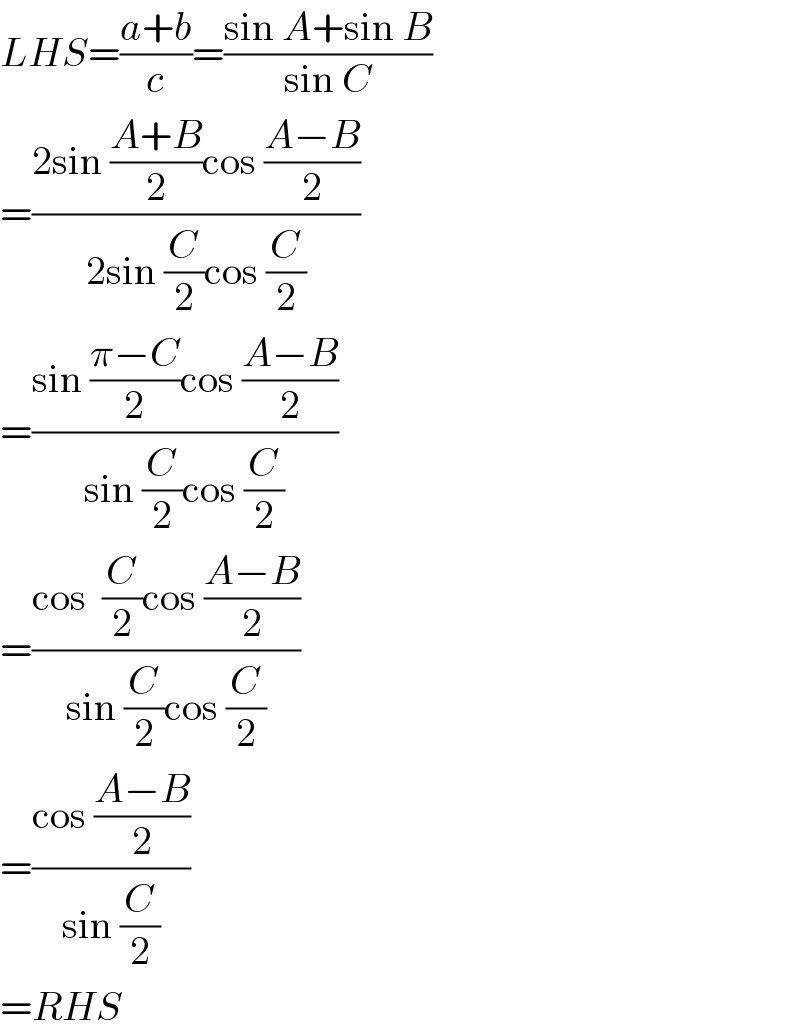
$${LHS}=\frac{{a}+{b}}{{c}}=\frac{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}}{\mathrm{sin}\:{C}} \\ $$$$=\frac{\mathrm{2sin}\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}}{\mathrm{2sin}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{sin}\:\frac{\pi−{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}}{\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{cos}\:\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}}{\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}}{\mathrm{sin}\:\frac{{C}}{\mathrm{2}}} \\ $$$$={RHS} \\ $$
Answered by behi83417@gmail.com last updated on 30/Sep/19
![cos(A/2)=(√((p(p−a))/(bc))),sin(A/2)=(√(((p−b)(p−c))/(bc))) cos((A−B)/2)=(√((p(p−a))/(bc))).(√((p(p−b))/(ac)))+ +(√(((p−b)(p−c))/(bc)))(√(((p−a)(p−c))/(ac)))= =(1/c)[p(√(((p−a)(p−b))/(ab)))+(p−c)(√(((p−a)(p−b))/(ab)))]= =((2p−c)/c)(√(((p−a)(p−b))/(ab)))=((a+b)/c).sin(C/2). please check the question sir.](https://www.tinkutara.com/question/Q70087.png)
$$\mathrm{cos}\frac{\mathrm{A}}{\mathrm{2}}=\sqrt{\frac{\mathrm{p}\left(\mathrm{p}−\mathrm{a}\right)}{\mathrm{bc}}},\mathrm{sin}\frac{\mathrm{A}}{\mathrm{2}}=\sqrt{\frac{\left(\mathrm{p}−\mathrm{b}\right)\left(\mathrm{p}−\mathrm{c}\right)}{\mathrm{bc}}} \\ $$$$\mathrm{cos}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}=\sqrt{\frac{\mathrm{p}\left(\mathrm{p}−\mathrm{a}\right)}{\mathrm{bc}}}.\sqrt{\frac{\mathrm{p}\left(\mathrm{p}−\mathrm{b}\right)}{\mathrm{ac}}}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\sqrt{\frac{\left(\mathrm{p}−\mathrm{b}\right)\left(\mathrm{p}−\mathrm{c}\right)}{\mathrm{bc}}}\sqrt{\frac{\left(\mathrm{p}−\mathrm{a}\right)\left(\mathrm{p}−\mathrm{c}\right)}{\mathrm{ac}}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{c}}\left[\mathrm{p}\sqrt{\frac{\left(\mathrm{p}−\mathrm{a}\right)\left(\mathrm{p}−\mathrm{b}\right)}{\mathrm{ab}}}+\left(\mathrm{p}−\mathrm{c}\right)\sqrt{\frac{\left(\mathrm{p}−\mathrm{a}\right)\left(\mathrm{p}−\mathrm{b}\right)}{\mathrm{ab}}}\right]= \\ $$$$=\frac{\mathrm{2p}−\mathrm{c}}{\mathrm{c}}\sqrt{\frac{\left(\mathrm{p}−\mathrm{a}\right)\left(\mathrm{p}−\mathrm{b}\right)}{\mathrm{ab}}}=\frac{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}}{\boldsymbol{\mathrm{c}}}.\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}. \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{the}\:\mathrm{question}\:\mathrm{sir}. \\ $$
