Question Number 69229 by naka3546 last updated on 21/Sep/19
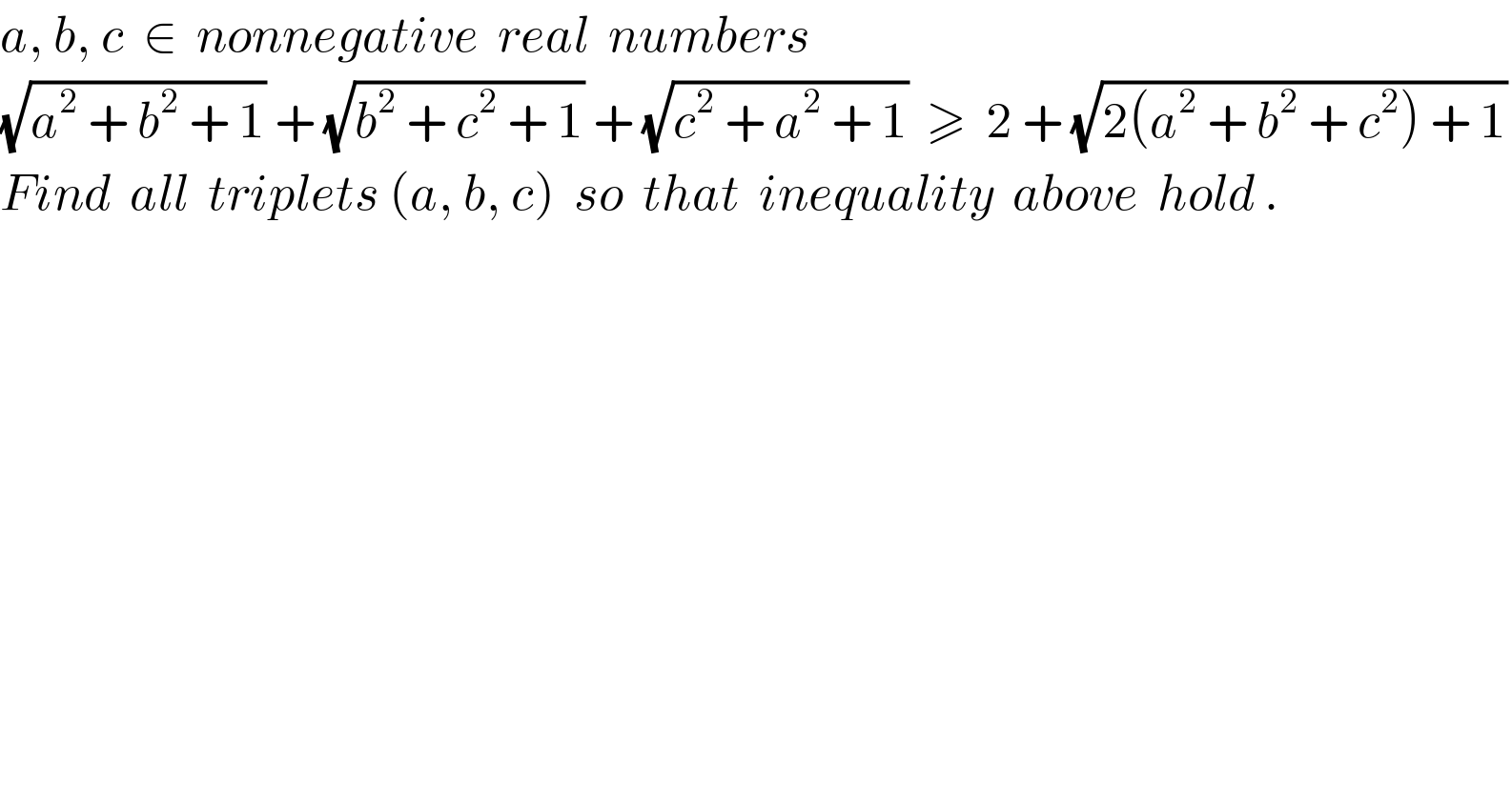
$${a},\:{b},\:{c}\:\:\in\:\:{nonnegative}\:\:{real}\:\:{numbers} \\ $$$$\sqrt{{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:\mathrm{1}}\:+\:\sqrt{{b}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \:+\:\mathrm{1}}\:+\:\sqrt{{c}^{\mathrm{2}} \:+\:{a}^{\mathrm{2}} \:+\:\mathrm{1}}\:\:\geqslant\:\:\mathrm{2}\:+\:\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \right)\:+\:\mathrm{1}} \\ $$$${Find}\:\:{all}\:\:{triplets}\:\left({a},\:{b},\:{c}\right)\:\:{so}\:\:{that}\:\:{inequality}\:\:{above}\:\:{hold}\:. \\ $$
