Question Number 139644 by mathdanisur last updated on 30/Apr/21
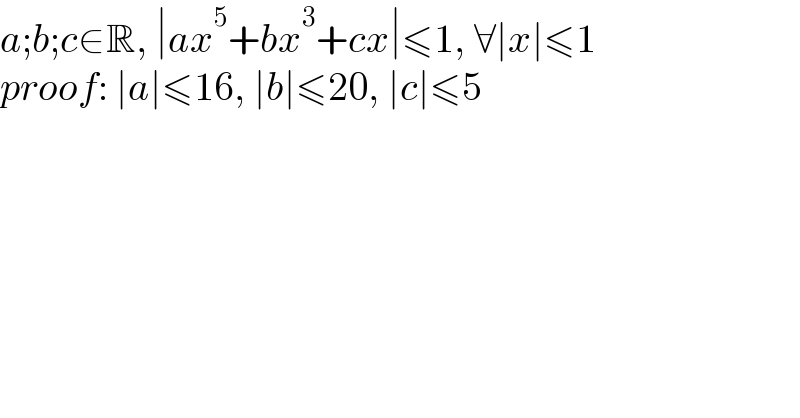
$${a};{b};{c}\in\mathbb{R},\:\mid{ax}^{\mathrm{5}} +{bx}^{\mathrm{3}} +{cx}\mid\leqslant\mathrm{1},\:\forall\mid{x}\mid\leqslant\mathrm{1} \\ $$$${proof}:\:\mid{a}\mid\leqslant\mathrm{16},\:\mid{b}\mid\leqslant\mathrm{20},\:\mid{c}\mid\leqslant\mathrm{5} \\ $$
Answered by ajfour last updated on 30/Apr/21
![let ∣x∣=r x=rcos θ+irsin θ ∣ar^5 e^(5iθ) +br^3 e^(3iθ) +cre^(iθ) ∣≤1 r^3 ∣ar^2 e^(2iθ) +b+(c/(r^2 e^(2iθ) ))∣≤1 r^3 ∣ar^2 (cos 2θ+isin 2θ)+b +(c/r^2 )(cos 2θ−isin 2θ)∣≤1 r^6 {[b+(ar^2 +(c/r^2 ))cos 2θ]^2 +(ar^2 −(c/r^2 ))^2 sin^2 2θ}≤1 r^6 {b^2 +2b(ar^2 +(c/r^2 ))cos 2θ +4accos^2 2θ+(ar^2 −(c/r^2 ))^2 }≤1 r^6 {b^2 +4ac[cos 2θ+(b/(4ac))(ar^2 +(c/r^2 ))]^2 −(b^2 /(4ac))(ar^2 +(c/r^2 ))^2 }≤1 ......](https://www.tinkutara.com/question/Q139646.png)
$${let}\:\:\mid{x}\mid={r} \\ $$$${x}={r}\mathrm{cos}\:\theta+{ir}\mathrm{sin}\:\theta \\ $$$$\mid{ar}^{\mathrm{5}} {e}^{\mathrm{5}{i}\theta} +{br}^{\mathrm{3}} {e}^{\mathrm{3}{i}\theta} +{cre}^{{i}\theta} \mid\leqslant\mathrm{1} \\ $$$${r}^{\mathrm{3}} \mid{ar}^{\mathrm{2}} {e}^{\mathrm{2}{i}\theta} +{b}+\frac{{c}}{{r}^{\mathrm{2}} {e}^{\mathrm{2}{i}\theta} }\mid\leqslant\mathrm{1} \\ $$$${r}^{\mathrm{3}} \mid{ar}^{\mathrm{2}} \left(\mathrm{cos}\:\mathrm{2}\theta+{i}\mathrm{sin}\:\mathrm{2}\theta\right)+{b} \\ $$$$\:\:\:\:\:\:\:\:+\frac{{c}}{{r}^{\mathrm{2}} }\left(\mathrm{cos}\:\mathrm{2}\theta−{i}\mathrm{sin}\:\mathrm{2}\theta\right)\mid\leqslant\mathrm{1} \\ $$$${r}^{\mathrm{6}} \left\{\left[{b}+\left({ar}^{\mathrm{2}} +\frac{{c}}{{r}^{\mathrm{2}} }\right)\mathrm{cos}\:\mathrm{2}\theta\right]^{\mathrm{2}} +\left({ar}^{\mathrm{2}} −\frac{{c}}{{r}^{\mathrm{2}} }\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta\right\}\leqslant\mathrm{1} \\ $$$${r}^{\mathrm{6}} \left\{{b}^{\mathrm{2}} +\mathrm{2}{b}\left({ar}^{\mathrm{2}} +\frac{{c}}{{r}^{\mathrm{2}} }\right)\mathrm{cos}\:\mathrm{2}\theta\right. \\ $$$$\left.\:\:\:\:\:\:\:+\mathrm{4}{ac}\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta+\left({ar}^{\mathrm{2}} −\frac{{c}}{{r}^{\mathrm{2}} }\right)^{\mathrm{2}} \right\}\leqslant\mathrm{1} \\ $$$${r}^{\mathrm{6}} \left\{{b}^{\mathrm{2}} +\mathrm{4}{ac}\left[\mathrm{cos}\:\mathrm{2}\theta+\frac{{b}}{\mathrm{4}{ac}}\left({ar}^{\mathrm{2}} +\frac{{c}}{{r}^{\mathrm{2}} }\right)\right]^{\mathrm{2}} \right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{ac}}\left({ar}^{\mathrm{2}} +\frac{{c}}{{r}^{\mathrm{2}} }\right)^{\mathrm{2}} \right\}\leqslant\mathrm{1} \\ $$$$…… \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 30/Apr/21

$${then}\:{how}\:{sir} \\ $$
Commented by mathdanisur last updated on 13/May/21

$${Ajfour}\:{Sir}\:{continuo}\:{please}… \\ $$
