Question Number 139248 by ajfour last updated on 24/Apr/21
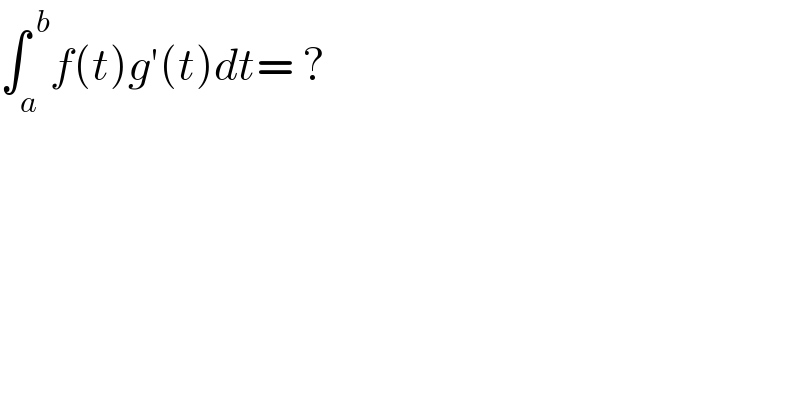
$$\int_{{a}} ^{\:{b}} {f}\left({t}\right){g}'\left({t}\right){dt}=\:? \\ $$
Answered by mathmax by abdo last updated on 25/Apr/21
![∫_a ^b f(t)g^′ (t)dt =[f(t)g(t)]_a ^b −∫_a ^b f^′ (t)g(t)dt =f(b)g(b)−f(a)g(a)−∫_a ^b f′(t)g(t)dt](https://www.tinkutara.com/question/Q139261.png)
$$\int_{\mathrm{a}} ^{\mathrm{b}} \:\mathrm{f}\left(\mathrm{t}\right)\mathrm{g}^{'} \left(\mathrm{t}\right)\mathrm{dt}\:=\left[\mathrm{f}\left(\mathrm{t}\right)\mathrm{g}\left(\mathrm{t}\right)\right]_{\mathrm{a}} ^{\mathrm{b}} −\int_{\mathrm{a}} ^{\mathrm{b}} \:\mathrm{f}^{'} \left(\mathrm{t}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\mathrm{f}\left(\mathrm{b}\right)\mathrm{g}\left(\mathrm{b}\right)−\mathrm{f}\left(\mathrm{a}\right)\mathrm{g}\left(\mathrm{a}\right)−\int_{\mathrm{a}} ^{\mathrm{b}} \:\mathrm{f}'\left(\mathrm{t}\right)\mathrm{g}\left(\mathrm{t}\right)\mathrm{dt} \\ $$
Answered by physicstutes last updated on 24/Apr/21
![u = f(t) and dv = g′(t)dt ⇒ du = f ′(t)dt and v = g(t) ⇒ [g(t) f(t)]_a ^b −∫_a ^b g(t) f′(t)dt I = ∫_a ^b g(t)f ′(t) dt = [g(t)f(t)]_a ^b −∫_a ^b f(t)g′(t)dt ⇒ ∫_a ^b f(t)g′(t)dt = [g(t)f(t)]_a ^b −{[g(t)f(t)]_a ^b −∫_a ^b f(t)g′(t)dt} determinant (((∫_a ^b f(t)g′(t)dt = 0))) determinant ((),())](https://www.tinkutara.com/question/Q139249.png)
$${u}\:=\:{f}\left({t}\right)\:\mathrm{and}\:{dv}\:=\:\mathrm{g}'\left({t}\right){dt} \\ $$$$\Rightarrow\:{du}\:=\:{f}\:'\left({t}\right){dt}\:\mathrm{and}\:{v}\:=\:\mathrm{g}\left({t}\right) \\ $$$$\Rightarrow\:\left[\mathrm{g}\left({t}\right)\:{f}\left({t}\right)\right]_{{a}} ^{{b}} −\int_{{a}} ^{{b}} \mathrm{g}\left({t}\right)\:{f}'\left({t}\right){dt} \\ $$$${I}\:=\:\int_{{a}} ^{{b}} \mathrm{g}\left({t}\right){f}\:'\left({t}\right)\:{dt}\:=\:\left[\mathrm{g}\left({t}\right){f}\left({t}\right)\right]_{{a}} ^{{b}} −\int_{{a}} ^{{b}} {f}\left({t}\right)\mathrm{g}'\left({t}\right){dt} \\ $$$$\Rightarrow\:\int_{{a}} ^{{b}} {f}\left({t}\right)\mathrm{g}'\left({t}\right){dt}\:=\:\left[\mathrm{g}\left({t}\right){f}\left({t}\right)\right]_{{a}} ^{{b}} −\left\{\left[\mathrm{g}\left({t}\right){f}\left({t}\right)\right]_{{a}} ^{{b}} −\int_{{a}} ^{{b}} {f}\left({t}\right)\mathrm{g}'\left({t}\right){dt}\right\} \\ $$$$\:\begin{array}{|c|}{\int_{{a}} ^{{b}} {f}\left({t}\right)\mathrm{g}'\left({t}\right){dt}\:=\:\mathrm{0}}\\\hline\end{array}\begin{array}{|c|c|}\\\\\hline\end{array} \\ $$
Commented by mr W last updated on 24/Apr/21
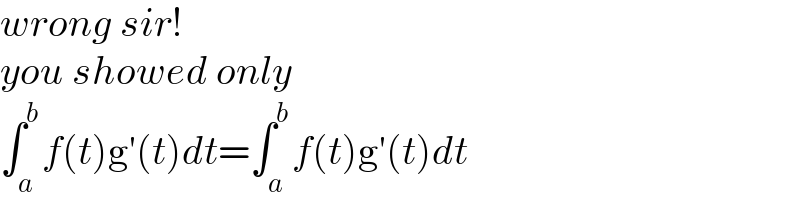
$${wrong}\:{sir}! \\ $$$${you}\:{showed}\:{only} \\ $$$$\int_{{a}} ^{{b}} {f}\left({t}\right)\mathrm{g}'\left({t}\right){dt}=\int_{{a}} ^{{b}} {f}\left({t}\right)\mathrm{g}'\left({t}\right){dt} \\ $$
Commented by mr W last updated on 24/Apr/21
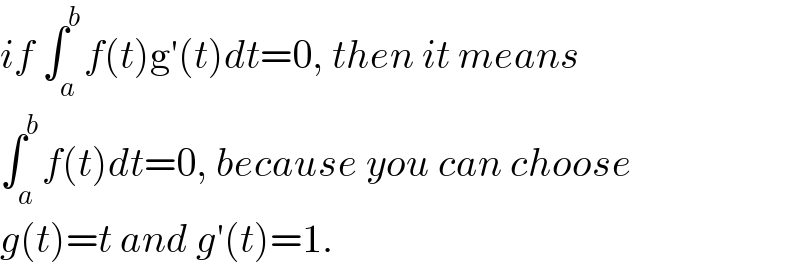
$${if}\:\int_{{a}} ^{{b}} {f}\left({t}\right)\mathrm{g}'\left({t}\right){dt}=\mathrm{0},\:{then}\:{it}\:{means} \\ $$$$\int_{{a}} ^{{b}} {f}\left({t}\right){dt}=\mathrm{0},\:{because}\:{you}\:{can}\:{choose} \\ $$$${g}\left({t}\right)={t}\:{and}\:{g}'\left({t}\right)=\mathrm{1}. \\ $$
