Menu Close

a-b-R-a-b-n-k-0-n-n-k-a-k-b-n-k-demontration-

Tinku Tara 0 Comments
Pin




Question Number 136783 by Abdoulaye last updated on 26/Mar/21
a,b∈R (a+b)^n =Σ_(k=0) ^n ((n),(k) )a^k b^(n−k) demontration!
$${a},{b}\in{R} \\ $$$$\left({a}+{b}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{k}} {b}^{{n}−{k}} \\ $$$${demontration}! \\ $$
Commented by mr W last updated on 26/Mar/21
(a+b)^n =Σ_(k=0) ^n ((n),(k) )a^(n−k) b^k =Σ_(k=0) ^n ((n),(k) )a^k b^(n−k)
$$\left({a}+{b}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{\mathrm{n}−\mathrm{k}} {b}^{{k}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{\mathrm{k}} {b}^{{n}−{k}} \\ $$
Commented by abdurehime last updated on 26/Mar/21
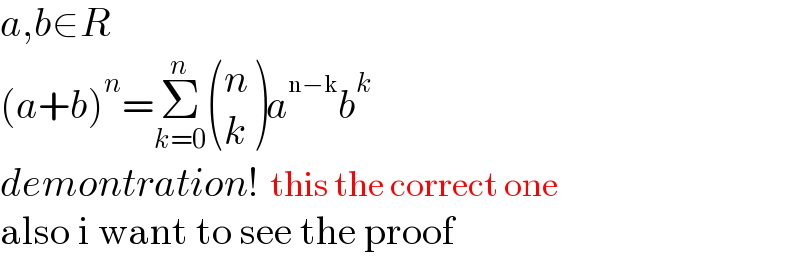
a,b∈R (a+b)^n =Σ_(k=0) ^n ((n),(k) )a^(n−k) b^k demontration! this the correct one also i want to see the proof
$${a},{b}\in{R} \\ $$$$\left({a}+{b}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{\mathrm{n}−\mathrm{k}} {b}^{{k}} \\ $$$${demontration}!\:\:\mathrm{this}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{one} \\ $$$$\mathrm{also}\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{see}\:\mathrm{the}\:\mathrm{proof} \\ $$
Answered by mr W last updated on 26/Mar/21
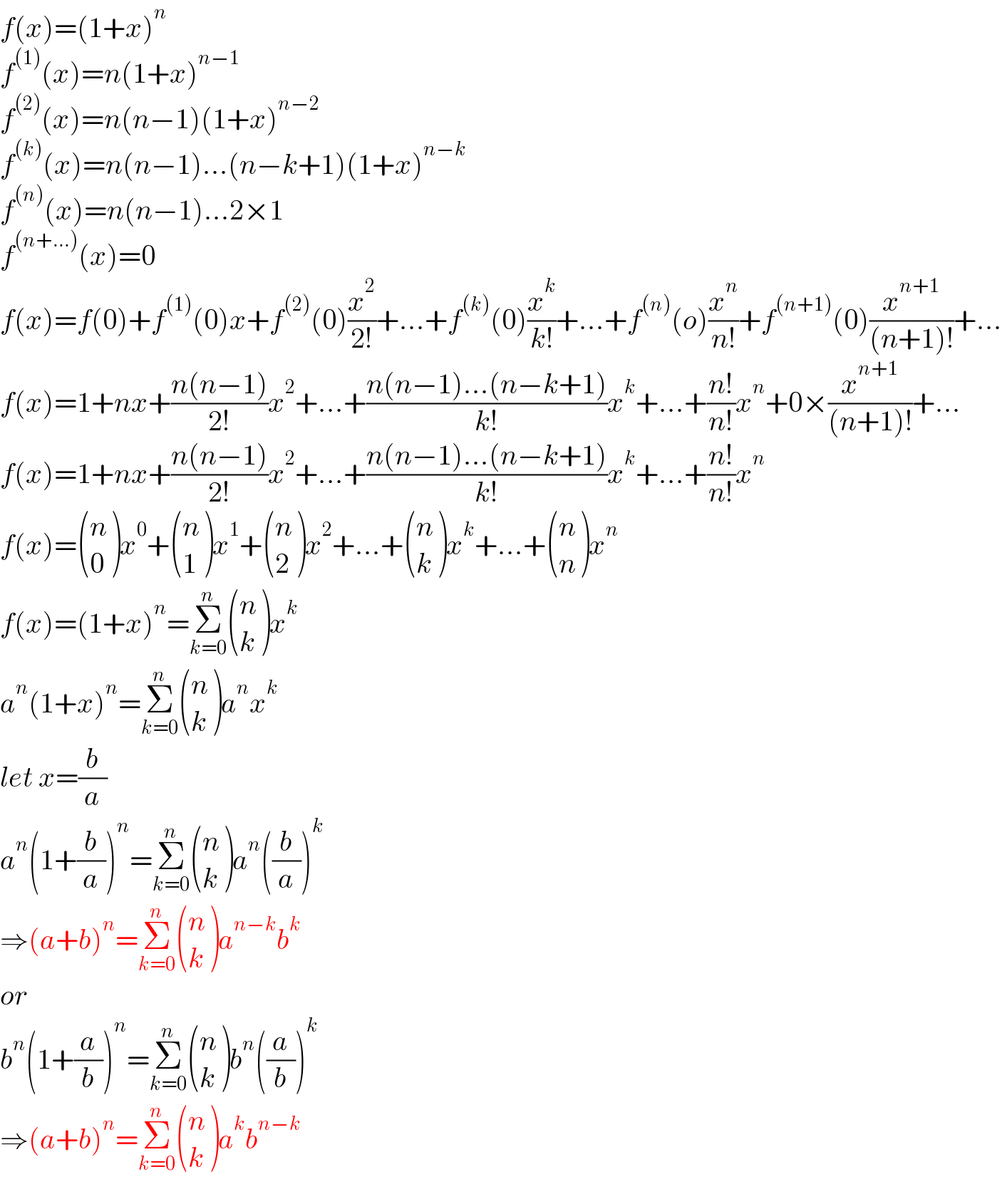
f(x)=(1+x)^n f^((1)) (x)=n(1+x)^(n−1) f^((2)) (x)=n(n−1)(1+x)^(n−2) f^((k)) (x)=n(n−1)...(n−k+1)(1+x)^(n−k) f^((n)) (x)=n(n−1)...2×1 f^((n+...)) (x)=0 f(x)=f(0)+f^((1)) (0)x+f^((2)) (0)(x^2 /(2!))+...+f^((k)) (0)(x^k /(k!))+...+f^((n)) (o)(x^n /(n!))+f^((n+1)) (0)(x^(n+1) /((n+1)!))+... f(x)=1+nx+((n(n−1))/(2!))x^2 +...+((n(n−1)...(n−k+1))/(k!))x^k +...+((n!)/(n!))x^n +0×(x^(n+1) /((n+1)!))+... f(x)=1+nx+((n(n−1))/(2!))x^2 +...+((n(n−1)...(n−k+1))/(k!))x^k +...+((n!)/(n!))x^n f(x)= ((n),(0) )x^0 + ((n),(1) )x^1 + ((n),(2) )x^2 +...+ ((n),(k) )x^k +...+ ((n),(n) )x^n f(x)=(1+x)^n =Σ_(k=0) ^n ((n),(k) )x^k a^n (1+x)^n =Σ_(k=0) ^n ((n),(k) )a^n x^k let x=(b/a) a^n (1+(b/a))^n =Σ_(k=0) ^n ((n),(k) )a^n ((b/a))^k ⇒(a+b)^n =Σ_(k=0) ^n ((n),(k) )a^(n−k) b^k or b^n (1+(a/b))^n =Σ_(k=0) ^n ((n),(k) )b^n ((a/b))^k ⇒(a+b)^n =Σ_(k=0) ^n ((n),(k) )a^k b^(n−k)
$${f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{n}} \\ $$$${f}^{\left(\mathrm{1}\right)} \left({x}\right)={n}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{1}} \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)={n}\left({n}−\mathrm{1}\right)\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{2}} \\ $$$${f}^{\left({k}\right)} \left({x}\right)={n}\left({n}−\mathrm{1}\right)…\left({n}−{k}+\mathrm{1}\right)\left(\mathrm{1}+{x}\right)^{{n}−{k}} \\ $$$${f}^{\left({n}\right)} \left({x}\right)={n}\left({n}−\mathrm{1}\right)…\mathrm{2}×\mathrm{1} \\ $$$${f}^{\left({n}+…\right)} \left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)+{f}^{\left(\mathrm{1}\right)} \left(\mathrm{0}\right){x}+{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+…+{f}^{\left({k}\right)} \left(\mathrm{0}\right)\frac{{x}^{{k}} }{{k}!}+…+{f}^{\left({n}\right)} \left({o}\right)\frac{{x}^{{n}} }{{n}!}+{f}^{\left({n}+\mathrm{1}\right)} \left(\mathrm{0}\right)\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}+… \\ $$$${f}\left({x}\right)=\mathrm{1}+{nx}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +…+\frac{{n}\left({n}−\mathrm{1}\right)…\left({n}−{k}+\mathrm{1}\right)}{{k}!}{x}^{{k}} +…+\frac{{n}!}{{n}!}{x}^{{n}} +\mathrm{0}×\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}+… \\ $$$${f}\left({x}\right)=\mathrm{1}+{nx}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +…+\frac{{n}\left({n}−\mathrm{1}\right)…\left({n}−{k}+\mathrm{1}\right)}{{k}!}{x}^{{k}} +…+\frac{{n}!}{{n}!}{x}^{{n}} \\ $$$${f}\left({x}\right)=\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}{x}^{\mathrm{0}} +\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}{x}^{\mathrm{1}} +\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}{x}^{\mathrm{2}} +…+\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{k}} +…+\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}{x}^{{n}} \\ $$$${f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{x}^{{k}} \\ $$$${a}^{{n}} \left(\mathrm{1}+{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{n}} {x}^{{k}} \\ $$$${let}\:{x}=\frac{{b}}{{a}} \\ $$$${a}^{{n}} \left(\mathrm{1}+\frac{{b}}{{a}}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{n}} \left(\frac{{b}}{{a}}\right)^{{k}} \\ $$$$\Rightarrow\left({a}+{b}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{n}−{k}} {b}^{{k}} \\ $$$${or} \\ $$$${b}^{{n}} \left(\mathrm{1}+\frac{{a}}{{b}}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{b}^{{n}} \left(\frac{{a}}{{b}}\right)^{{k}} \\ $$$$\Rightarrow\left({a}+{b}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{k}} {b}^{{n}−{k}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *