Question Number 9988 by konen last updated on 20/Jan/17
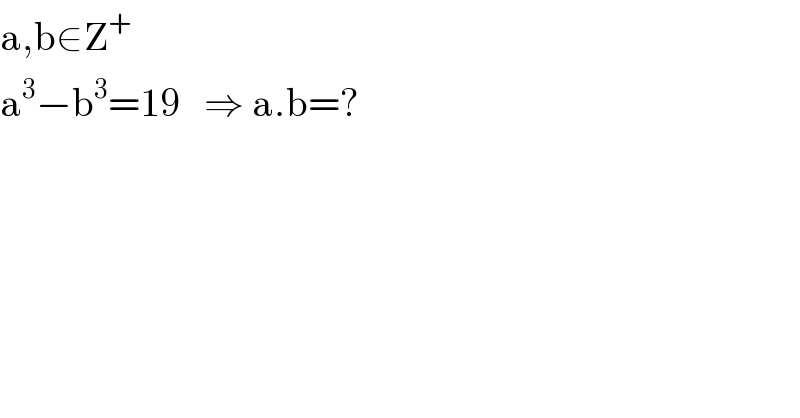
$$\mathrm{a},\mathrm{b}\in\mathrm{Z}^{+} \\ $$$$\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} =\mathrm{19}\:\:\:\Rightarrow\:\mathrm{a}.\mathrm{b}=? \\ $$
Answered by mrW1 last updated on 20/Jan/17
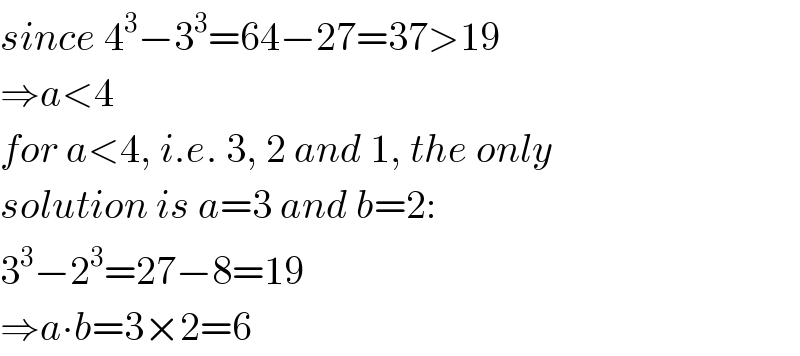
$${since}\:\mathrm{4}^{\mathrm{3}} −\mathrm{3}^{\mathrm{3}} =\mathrm{64}−\mathrm{27}=\mathrm{37}>\mathrm{19} \\ $$$$\Rightarrow{a}<\mathrm{4} \\ $$$${for}\:{a}<\mathrm{4},\:{i}.{e}.\:\mathrm{3},\:\mathrm{2}\:{and}\:\mathrm{1},\:{the}\:{only} \\ $$$${solution}\:{is}\:{a}=\mathrm{3}\:{and}\:{b}=\mathrm{2}: \\ $$$$\mathrm{3}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} =\mathrm{27}−\mathrm{8}=\mathrm{19} \\ $$$$\Rightarrow{a}\centerdot{b}=\mathrm{3}×\mathrm{2}=\mathrm{6} \\ $$
Commented by RasheedSoomro last updated on 20/Jan/17

$$\mathcal{A}{lso}\:\mathcal{G}{ood}! \\ $$
Answered by nume1114 last updated on 20/Jan/17
![a^3 −b^3 =(a−b)(a^2 +ab+b^2 )=19 a,b∈Z^+ ⇒a−b<a^2 +ab+b^2 , and 19 is prime ⇒a−b=1,a^2 +ab+b^2 =19 ab=(1/3)[(a^2 +ab+b^2 )−(a−b)^2 ] =(1/3)(19−1^2 ) =6](https://www.tinkutara.com/question/Q9998.png)
$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)=\mathrm{19} \\ $$$${a},{b}\in\mathbb{Z}^{+} \Rightarrow{a}−{b}<{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \:, \\ $$$$\mathrm{and}\:\mathrm{19}\:\mathrm{is}\:\mathrm{prime} \\ $$$$\Rightarrow{a}−{b}=\mathrm{1},{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} =\mathrm{19} \\ $$$${ab}=\frac{\mathrm{1}}{\mathrm{3}}\left[\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)−\left({a}−{b}\right)^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{19}−\mathrm{1}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:=\mathrm{6} \\ $$
Commented by mrW1 last updated on 20/Jan/17
$${very}\:{good}\:{method}! \\ $$
Commented by RasheedSoomro last updated on 20/Jan/17
$$\mathcal{A}\:\mathcal{N}{ovel}\:\mathcal{M}{ethod}! \\ $$
