Question Number 9962 by konen last updated on 19/Jan/17
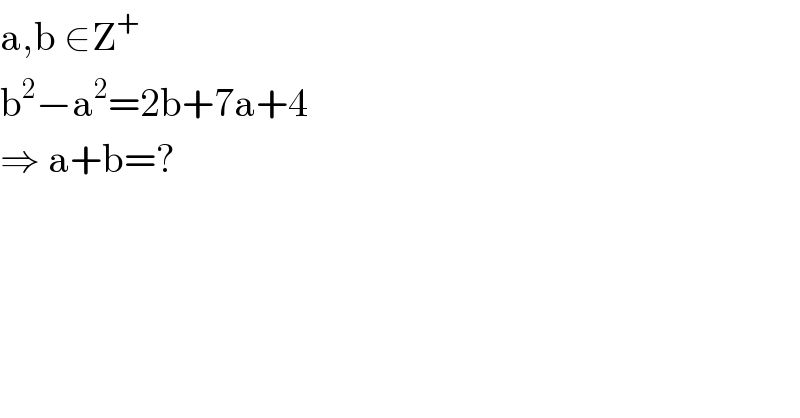
$$\mathrm{a},\mathrm{b}\:\in\mathrm{Z}^{+} \\ $$$$\mathrm{b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} =\mathrm{2b}+\mathrm{7a}+\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{a}+\mathrm{b}=? \\ $$
Commented by prakash jain last updated on 19/Jan/17
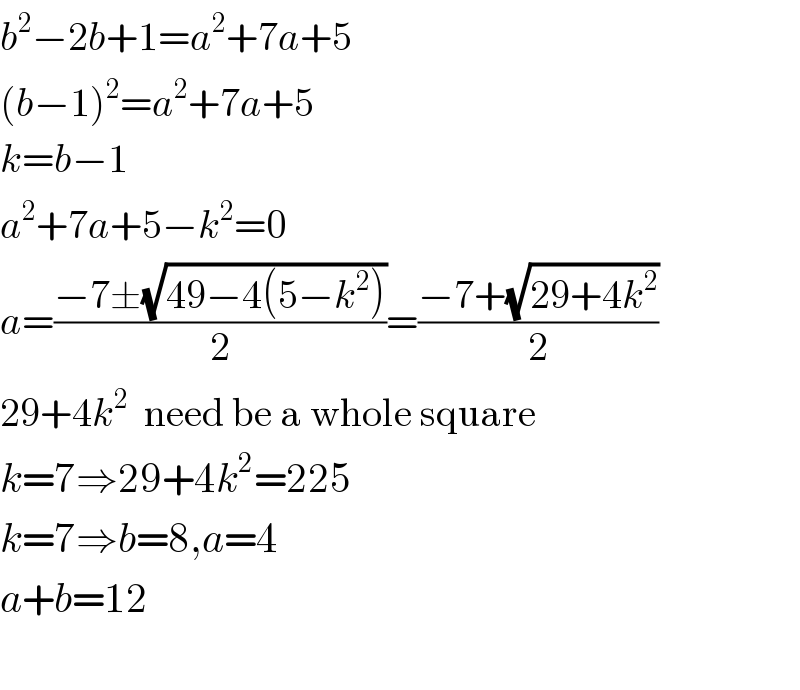
$${b}^{\mathrm{2}} −\mathrm{2}{b}+\mathrm{1}={a}^{\mathrm{2}} +\mathrm{7}{a}+\mathrm{5} \\ $$$$\left({b}−\mathrm{1}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{7}{a}+\mathrm{5} \\ $$$${k}={b}−\mathrm{1} \\ $$$${a}^{\mathrm{2}} +\mathrm{7}{a}+\mathrm{5}−{k}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}=\frac{−\mathrm{7}\pm\sqrt{\mathrm{49}−\mathrm{4}\left(\mathrm{5}−{k}^{\mathrm{2}} \right)}}{\mathrm{2}}=\frac{−\mathrm{7}+\sqrt{\mathrm{29}+\mathrm{4}{k}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{29}+\mathrm{4}{k}^{\mathrm{2}} \:\:\mathrm{need}\:\mathrm{be}\:\mathrm{a}\:\mathrm{whole}\:\mathrm{square} \\ $$$${k}=\mathrm{7}\Rightarrow\mathrm{29}+\mathrm{4}{k}^{\mathrm{2}} =\mathrm{225} \\ $$$${k}=\mathrm{7}\Rightarrow{b}=\mathrm{8},{a}=\mathrm{4} \\ $$$${a}+{b}=\mathrm{12} \\ $$$$ \\ $$
Commented by prakash jain last updated on 19/Jan/17
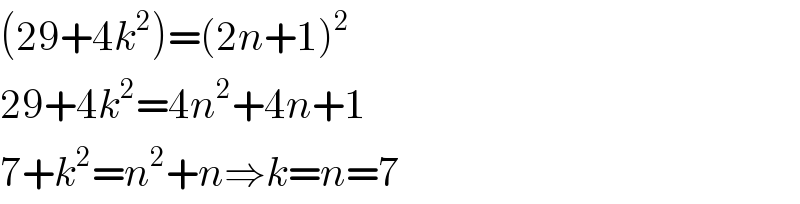
$$\left(\mathrm{29}+\mathrm{4}{k}^{\mathrm{2}} \right)=\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{29}+\mathrm{4}{k}^{\mathrm{2}} =\mathrm{4}{n}^{\mathrm{2}} +\mathrm{4}{n}+\mathrm{1} \\ $$$$\mathrm{7}+{k}^{\mathrm{2}} ={n}^{\mathrm{2}} +{n}\Rightarrow{k}={n}=\mathrm{7} \\ $$
