Question Number 135558 by bemath last updated on 14/Mar/21

$$ \\ $$A boy throws a ball at a vertical wall 4 m away. The ball is 2 m above ground when it leaves the girl's hand with initial velocity of 10√2 𝑚/𝑠 at 45º. Horizontal component is reversed only. Where does the ball hit the ground after bounce?
Commented by mr W last updated on 14/Mar/21
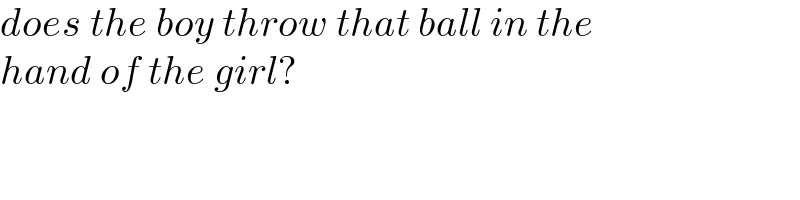
$${does}\:{the}\:{boy}\:{throw}\:{that}\:{ball}\:{in}\:{the} \\ $$$${hand}\:{of}\:{the}\:{girl}? \\ $$
Answered by mr W last updated on 14/Mar/21
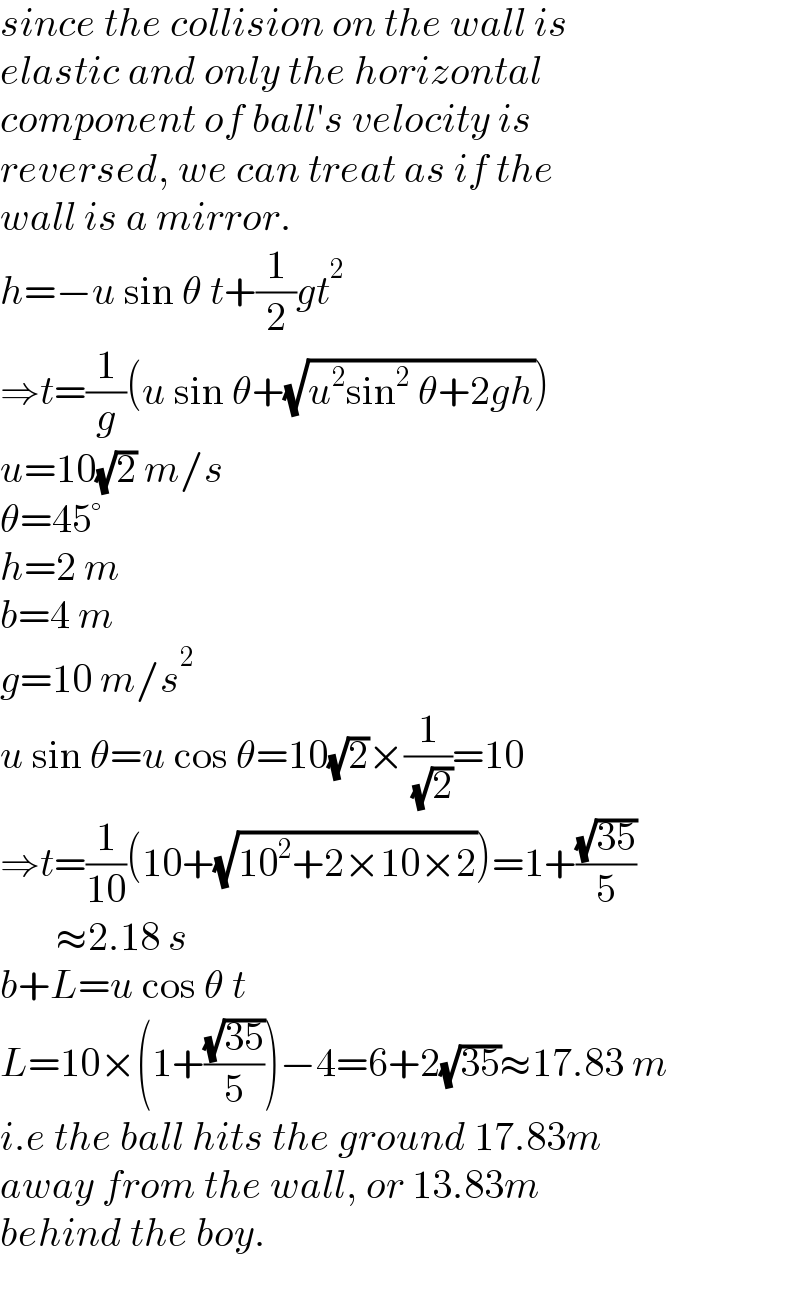
$${since}\:{the}\:{collision}\:{on}\:{the}\:{wall}\:{is} \\ $$$${elastic}\:{and}\:{only}\:{the}\:{horizontal} \\ $$$${component}\:{of}\:{ball}'{s}\:{velocity}\:{is} \\ $$$${reversed},\:{we}\:{can}\:{treat}\:{as}\:{if}\:{the} \\ $$$${wall}\:{is}\:{a}\:{mirror}. \\ $$$${h}=−{u}\:\mathrm{sin}\:\theta\:{t}+\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{{g}}\left({u}\:\mathrm{sin}\:\theta+\sqrt{{u}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}{gh}}\right) \\ $$$${u}=\mathrm{10}\sqrt{\mathrm{2}}\:{m}/{s} \\ $$$$\theta=\mathrm{45}° \\ $$$${h}=\mathrm{2}\:{m} \\ $$$${b}=\mathrm{4}\:{m} \\ $$$${g}=\mathrm{10}\:{m}/{s}^{\mathrm{2}} \\ $$$${u}\:\mathrm{sin}\:\theta={u}\:\mathrm{cos}\:\theta=\mathrm{10}\sqrt{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\mathrm{10} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{10}+\sqrt{\mathrm{10}^{\mathrm{2}} +\mathrm{2}×\mathrm{10}×\mathrm{2}}\right)=\mathrm{1}+\frac{\sqrt{\mathrm{35}}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\approx\mathrm{2}.\mathrm{18}\:{s} \\ $$$${b}+{L}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${L}=\mathrm{10}×\left(\mathrm{1}+\frac{\sqrt{\mathrm{35}}}{\mathrm{5}}\right)−\mathrm{4}=\mathrm{6}+\mathrm{2}\sqrt{\mathrm{35}}\approx\mathrm{17}.\mathrm{83}\:{m} \\ $$$${i}.{e}\:{the}\:{ball}\:{hits}\:{the}\:{ground}\:\mathrm{17}.\mathrm{83}{m} \\ $$$${away}\:{from}\:{the}\:{wall},\:{or}\:\mathrm{13}.\mathrm{83}{m} \\ $$$${behind}\:{the}\:{boy}. \\ $$
Commented by mr W last updated on 14/Mar/21
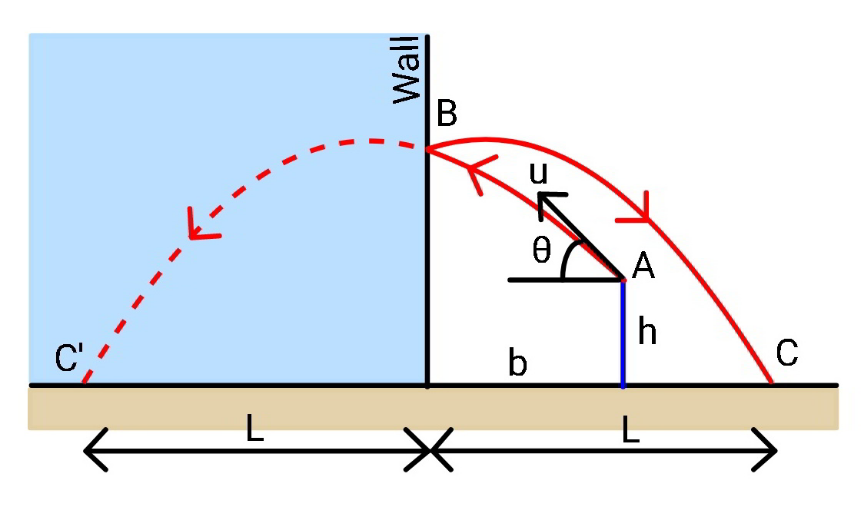
Commented by bemath last updated on 14/Mar/21

$${yes}…{sir}…{nice} \\ $$
