Menu Close

A-circular-disc-of-mass-20kg-and-radius-15cm-is-mounted-in-an-horizontal-cylinder-axel-of-radius-1-5cm-Calculate-the-kinectic-energy-of-the-disc-after-1-2-secs-if-a-force-of-12N-is-applied-tangential

Tinku Tara 0 Comments
Pin




Question Number 10640 by Saham last updated on 21/Feb/17
A circular disc of mass 20kg and radius 15cm is mounted in an horizontal cylinder axel of radius 1.5cm, Calculate the kinectic energy of the disc after 1.2 secs if a force of 12N is applied tangentially to the axel.
$$\mathrm{A}\:\mathrm{circular}\:\mathrm{disc}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{20kg}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{15cm}\:\mathrm{is}\:\mathrm{mounted}\:\mathrm{in}\:\mathrm{an} \\ $$$$\mathrm{horizontal}\:\mathrm{cylinder}\:\mathrm{axel}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{1}.\mathrm{5cm},\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{kinectic} \\ $$$$\mathrm{energy}\:\mathrm{of}\:\mathrm{the}\:\mathrm{disc}\:\mathrm{after}\:\mathrm{1}.\mathrm{2}\:\mathrm{secs}\:\mathrm{if}\:\mathrm{a}\:\mathrm{force}\:\mathrm{of}\:\mathrm{12N}\:\mathrm{is}\:\mathrm{applied}\:\mathrm{tangentially} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{axel}. \\ $$
Answered by mrW1 last updated on 21/Feb/17
moment of inertia I=(1/2)mr^2 =(1/2)×20×0.15^2 =0.225 kgm^2 torque T=Fr_1 =12×0.015=0.18 Nm with α=angular acceleration T=Iα ⇒α=(T/I)=((0.18)/(0.225))=0.8 rad/s^2 angular velocity ω=αt=0.8×1.2=0.96 rad/s kinetic energy KE=(1/2)Iω^2 =(1/2)×0.225×0.96^2 =0.10368 J or KE=work=Fs=Fθr_1 θ=(1/2)αt^2 =(1/2)×0.8×1.2^2 =0.576 rad ⇒KE=12×0.576×0.015=0.10368 J
$${moment}\:{of}\:{inertia}\:{I}=\frac{\mathrm{1}}{\mathrm{2}}{mr}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{20}×\mathrm{0}.\mathrm{15}^{\mathrm{2}} =\mathrm{0}.\mathrm{225}\:{kgm}^{\mathrm{2}} \\ $$$${torque}\:{T}={Fr}_{\mathrm{1}} =\mathrm{12}×\mathrm{0}.\mathrm{015}=\mathrm{0}.\mathrm{18}\:{Nm} \\ $$$$ \\ $$$${with}\:\alpha={angular}\:{acceleration} \\ $$$${T}={I}\alpha \\ $$$$\Rightarrow\alpha=\frac{{T}}{{I}}=\frac{\mathrm{0}.\mathrm{18}}{\mathrm{0}.\mathrm{225}}=\mathrm{0}.\mathrm{8}\:{rad}/{s}^{\mathrm{2}} \\ $$$$ \\ $$$${angular}\:{velocity} \\ $$$$\omega=\alpha{t}=\mathrm{0}.\mathrm{8}×\mathrm{1}.\mathrm{2}=\mathrm{0}.\mathrm{96}\:{rad}/{s} \\ $$$$ \\ $$$${kinetic}\:{energy} \\ $$$${KE}=\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}.\mathrm{225}×\mathrm{0}.\mathrm{96}^{\mathrm{2}} =\mathrm{0}.\mathrm{10368}\:{J} \\ $$$$ \\ $$$${or} \\ $$$${KE}={work}={Fs}={F}\theta{r}_{\mathrm{1}} \\ $$$$\theta=\frac{\mathrm{1}}{\mathrm{2}}\alpha{t}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}.\mathrm{8}×\mathrm{1}.\mathrm{2}^{\mathrm{2}} =\mathrm{0}.\mathrm{576}\:{rad} \\ $$$$\Rightarrow{KE}=\mathrm{12}×\mathrm{0}.\mathrm{576}×\mathrm{0}.\mathrm{015}=\mathrm{0}.\mathrm{10368}\:{J} \\ $$
Commented by Saham last updated on 21/Feb/17
wow. i really appreciate sir. God bless you.
$$\mathrm{wow}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Answered by remember last updated on 21/Feb/17
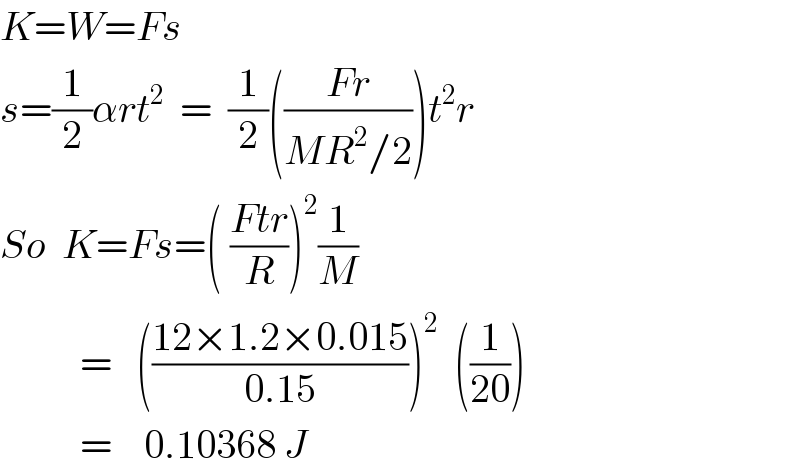
K=W=Fs s=(1/2)αrt^2 = (1/2)(((Fr)/(MR^2 /2)))t^2 r So K=Fs=( ((Ftr)/R))^2 (1/M) = (((12×1.2×0.015)/(0.15)))^2 ((1/(20))) = 0.10368 J
$${K}={W}={Fs} \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}\alpha{rt}^{\mathrm{2}} \:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{Fr}}{{MR}^{\mathrm{2}} /\mathrm{2}}\right){t}^{\mathrm{2}} {r} \\ $$$${So}\:\:{K}={Fs}=\left(\:\frac{{Ftr}}{{R}}\right)^{\mathrm{2}} \frac{\mathrm{1}}{{M}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\:\:\left(\frac{\mathrm{12}×\mathrm{1}.\mathrm{2}×\mathrm{0}.\mathrm{015}}{\mathrm{0}.\mathrm{15}}\right)^{\mathrm{2}} \:\:\left(\frac{\mathrm{1}}{\mathrm{20}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\:\:\:\mathrm{0}.\mathrm{10368}\:{J} \\ $$
Commented by remember last updated on 21/Feb/17
Commented by Saham last updated on 21/Feb/17
Great, i really appreciate.
$$\mathrm{Great},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *